ИНТЕРПОЛЯЦИЯ, ЭКСТРАПОЛЯЦИЯ И АНАЛИТИЧЕСКИЙ МЕТОД ВЫРАВНИВАНИЯ РЯДОВ ДИНАМИКИ.
Интерполяцияприменяется для определения величины промежуточных уровней на основе известных смежных уровней ряда.
Метод интерполяции применяется на известном предположении характера изменения уровней ряда динамики, который основывается на количественных оценках абсолютных приростов или темпов роста.
Если ряд динамики имеет примерно одинаковые цепные абсолютные приросты, то промежуточные неизвестные уровни ряда определяются по формуле:
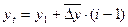
где 
- средний абсолютный прирост; 
- первый уровень ряда; i – порядковый номер уровня ряда.
Если ряд динамики имеет примерно одинаковые цепные темпы роста, то неизвестные промежуточные уровни ряда определяются по формуле: 
, где 
- средний темп роста.
Экстраполяция – это определение неизвестных уровней динамического ряда, лежащих за его пределами, т. е. либо будущих уровней, либо уровней, предшествующих начальному.
При экстраполяции исходят из предположения, что характер динамики, выявленный за определённый период времени, сохраняется и в будущем (или имеет место в прошлом).
Метод экстраполяции применяют чаще всего при прогнозировании будущих значений экономических явлений и процессов.
Если ряд динамики имеет примерно одинаковые цепные абсолютные приросты, то значения будущих уровней ряда определяются по формуле: 
,
где - средний абсолютный прирост; 
- значение последнего уровня ряда; i – срок прогноза (i = 1,2,…n)
|
|
|
Если ряд динамики имеет примерно одинаковые цепные темпы роста, то значения будущих уровней ряда определяются по формуле:
Метод аналитического выравнивания ряда динамикипозволяет получить аналитическую модель, выражающую основную тенденцию развития явления во времени.
В качестве вида аналитической модели могут быть приняты уравнения прямой линии, параболы, показательной функции и других видов.
Для установления вида аналитической модели применяются следующие методы:
1. Графический метод предусматривает нанесение на график фактических уровней ряда, где визуально подбирается форма кривой модели, которая наиболее соответствует реальному процессу. Если по фактическим уровням ряда тенденция чётко не выявляется, то проводят сглаживание ряда по скользящей средней.
2. Метод анализа показателей ряда динамики, который заключается в следующем:
а) если ряд динамики имеет примерно одинаковые цепные абсолютные приросты, то в качестве основной тенденции выбирается уравнение прямой линии: 
, где t – периоды времени;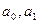 
- коэффициенты уравнения.
б) если ряд динамики имеет примерно одинаковые цепные темпы роста, то в качестве основной тенденции выбирается уравнение показательной функции, имеющей вид: 
|
|
|
в) если в ряду динамики цепные абсолютные приросты равномерно увеличиваются или уменьшаются, то в качестве основной тенденции выбирается уравнение параболы, имеющее вид: 
После выбора вида уравнения определяются его параметры методом наименьших квадратов. Сущность данного метода заключается в минимизации суммы квадратов отклонений фактических уравнений динамического ряда, от соответствующих им во времени, выровненных (расчётных) уровней, определённых по уравнению, т.е. 
, где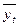 
- расчетные (теоретические) уровни ряда; y – фактические уровни ряда.
Для определения параметров уравнения прямой линии составляется и решается система из двух уравнений:
где n – число уровней ряда; t – периоды времени; y – фактические уровни ряда.
Для определения параметров уравнения параболы составляется и решается система из трёх уравнений:
Для упрощения решения системы уравнений переносят начало координат в середину динамического ряда, где 
, (k – нечетное число)
Для нечётного числа уровней ряда динамики:
t = …-3, -2, -1, 0, 1, 2, 3…
Для чётного числа уровней ряда динамики:
t =…-5, -3, -1, 1, 3, 5…
Дата добавления: 2018-05-02; просмотров: 1426; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!