Цепные и базисные индивидуальные индексы
Системы цепных и базисных индексов могут быть построены для индивидуальных и общих индексов. Пример системы индивидуальных индексов дан в табл. 5.
Таблица 5
| Название индивидуального индекса | Система индексов | |
| базисных | цепных | |
| Индекс стоимости |  ;  , ...,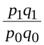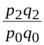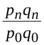 
| ;  , ..., 
|
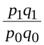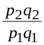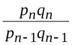
| Индекс физического объема |  ;  ; ...,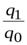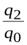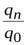 
| ;  ; ..., 
|
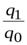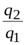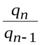
| Индекс цен |  ;  ; ...,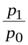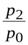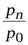 
| ;  ; ..., 
|
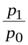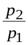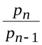
Между цепными и базисными индексами существует определенная взаимосвязь, что позволяет переходить от одних индексов к другим.
а) переход от цепных к базисным осуществляется перемножением последовательно цепные индексы, например:
= 
; 
= 
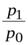
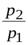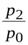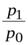
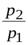
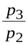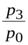и т.д.
а) переход от базисных к цепным осуществляется через отношение двух последовательных базисных индексов, например:
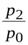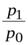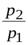: = и т.д.
Цепные и базисные общие (сводные) индексы
Если, например, известны данные по предприятию о выпуске q нескольких видов продукции (А, Б, В и т.д.) и о ценах р на нее за четыре периода, то при вычислении цепных и базисных общих индексов физического объема и цен можно по-разному решать вопрос о весах (соизмерителях).
Системой индексов с постоянными весами называется система общих (сводных) индексов одного и того же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому. Постоянные веса позволяют исключить влияние изменения структуры на величину индекса.
Примеры.
· Цепные индексы физического объема по агрегатной формуле (продукцию всех периодов можно оценить в одних и тех же ценах, предположим в ценах первого периода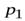 
, т.е.соизмерителем (весом) будет служить постоянная величина ):
|
|
|
= 
; 
= 
; 
= 
.
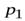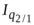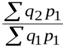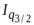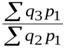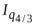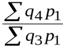· Цепные индексы цен (предположим, в качестве соизмерителя (веса) примем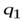 
):
= 
; 
= 
; 
= 
.
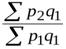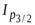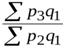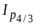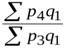Система индексов с переменными весами представляет собой систему общих (сводных) индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного индекса к другому. Переменные веса это веса отчетного периода.
Примеры.
· Вычисляя цепные индексы физического объема, можно было поступить так: для каждого периода строить индекс объема, принимая в качестве весов цены предыдущего периода:
= ; = 
; = 
.
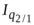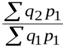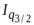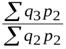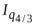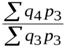· Цепные индексы цен (т.е. применяются веса текущего периода):
= 
; = 
; = 
.
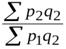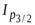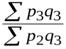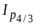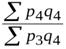Замечания.
1) Для общих (агрегатных) индексов переход от цепных индексов к базисным строго математически возможен лишь для индексов с постоянными весами (например, на основе записанных выше цепных индексов физического объема с постоянными весами путем перемножения их легко получить соответствующий базисный индекс физического объема, в частности: 
= 
).
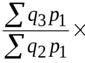
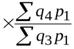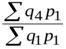2) При применении такого перехода (т.е. от цепных индексов к базисным) к индексам с переменными весами необходимо оговорить условность такого перехода и отметить, что структура (состав) «агрегата» (для которого вычисляется индекс) мало подвержена изменениям (отметим, это условие только предполагается).
|
|
|
СРЕДНЕВЗВЕШЕННЫЕ ИНДЕКСЫ.
Средневзвешенный индекс- это средний из индивидуальных индексов, взвешенных на объемы, имеющие одинаковую размерность и зафиксированные на неизменном уровне.
Средневзвешенный индекс физического объема вычисляется по формуле средней арифметической взвешенной и тождественен агрегатному индексу физического объема:
, где 
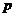- цена единицы продукции;
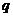- количество продукции;
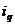- индивидуальный индекс количества продукции.
Средневзвешенный индекс цен вычисляется по формуле средней гармонической взвешенной и тождественен агрегатному индексу цен:
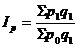
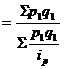, где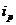 
- индивидуальный индекс количества продукции.
Пример 2
Динамика потребительских цен на отдельные товарные группы характеризуется следующими данными:
| Группа товаров | Товарооборот в фактических ценах, млн. ден. ед. | Темп прироста цен, % | |
| Базисный период | Отчетный период | ||
| Продовольственные | 526 | 583 | +6 |
| Непродовольственные | 424 | 255 | +2 |
Определите общий индекс цен.
|
|
|
Решение.
Для определения средневзвешенного индекса цен определим индивидуальные индексы цен:
| Группа товаров | Товарооборот в фактических ценах, млн. ден. ед. | Темп прироста цен, % | Индивидуальный индекс цен ( | |
Базисный период (  )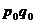
| Отчетный период (  )
| |||
| Продовольственные | 526 | 583 | +6 | (100+6)/100=1,06 |
| Непродовольственные | 424 | 255 | +2 | (100+2)/100=1,02 |
Рассчитаем средневзвешенный индекс цен:
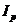
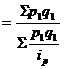
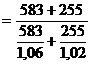
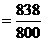= 1,0475 или 104,75%
Т.е. цены в среднем увеличились на 4,75%.
Дата добавления: 2018-05-02; просмотров: 703; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!