СРЕДНЯЯ И ПРЕДЕЛЬНАЯ ОШИБКИ ВЫБОРКИ.
Ошибки выборки (репрезентативности) – это разность между выборочной характеристикой показателя и генеральным параметром. Эти ошибки делятся на систематические и случайные.
Систематические ошибки возникают в результате нарушения принципа отбора. Их необходимо предусматривать в процессе планирования отбора.
Случайные ошибки имеют объективный характер и возникают в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. Их размер можно подсчитать на основании теории вероятности и её предельных теорем (П.Л. Чебышев и А.М. Ляпунов)
На минимизации случайных ошибок и построен выборочный метод наблюдений.
Пример №1
Из совокупности студентов произведены две 20%-ые выборки для изучения оценки.
Известны следующие данные об успеваемости студентов:
| Оценка | Генеральная совокупность | Выборочные совокупности | |
| первая | вторая | ||
| 2 | 200 | 35 | 45 |
| 3 | 500 | 90 | 110 |
| 4 | 200 | 50 | 35 |
| 5 | 100 | 25 | 10 |
| итого | 1000 | 200 | 200 |
Средняя в генеральной совокупности равна:

Доля отличников:
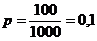
По данным первой выборки выборочная средняя и доля равны:
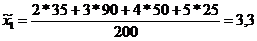
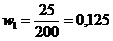
По данным второй выборки выборочная средняя и доля равны:
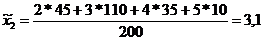
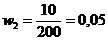
Выделяют:
1) ошибку средней 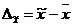
- для первой выборки 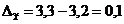
- для второй выборки 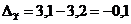
2) ошибку доли 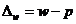
- для первой выборки 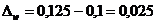
- для второй выборки 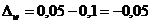
Таким образом, можно сделать вывод, что ошибки выборки являются переменными величинами и могут принимать различные значения. Поэтому рассчитывают среднюю из возможных ошибок μ.
|
|
|
Математически доказано, что например при случайном повторном отборе средняя ошибка определяется по следующей формуле:
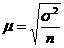 и т.д.
и т.д.
Но ошибка конкретной выборки может оказаться выше средней ошибки, поэтому рассчитывают предельную ошибку выборки:
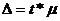 , где t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности P, выдержки из которой приведены ниже
, где t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности P, выдержки из которой приведены ниже
Выдержки из таблицы значений интегральной функции Лапласа при заданной доверительной вероятности Р
| P(t) | 0,683 | 0,95 | 0,954 | 0,99 | 0,997 |
| t | 1 | 1,96 | 2 | 2,58 | 3 |
Решим пример №2:
Методом собственно случайной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64%, а дисперсия составила 2,56.
Определить с вероятностью, равной 0,954, предельные значения генеральной средней.
Решение:
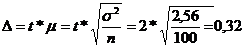
Генеральный параметр находится в следующих пределах: 
Для нашего примера: 
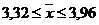 , т.е с вероятность 0,954 можно утверждать, что жирность молока в генеральной совокупности будет находится в пределах от 3,32% до 3,96%
, т.е с вероятность 0,954 можно утверждать, что жирность молока в генеральной совокупности будет находится в пределах от 3,32% до 3,96%
|
|
|

ОПРЕДЕЛЕНИЕ НЕОБХОДИМОЙ ЧИСЛЕННОСТИ ВЫБОРКИ
Формулы для определения необходимой численности выборки зависят от способа отбора, они различны для расчета средней и доли и следуют из формул предельных ошибок выборки:
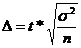 ―›
―› 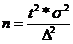
Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки ( 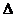 ) и доверительную вероятность (t), которые определяются как задачами , стоящими перед исследованиям, так и природой изучаемого явления. Неизвестной остается дисперсия признака, которая зависит от вариации, существующей объективно, независимо от исследователя и неизвестной к началу выборочного наблюдения.
) и доверительную вероятность (t), которые определяются как задачами , стоящими перед исследованиям, так и природой изучаемого явления. Неизвестной остается дисперсия признака, которая зависит от вариации, существующей объективно, независимо от исследователя и неизвестной к началу выборочного наблюдения.
Существуют следующие способы приближенного определения дисперсии:
1) использование дисперсии, рассчитанной в предыдущих исследованиях;
2) по правилу « трех сигм» общий размах вариации укладывается в 6σ, поэтому 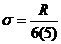 ;
;
3) если хотя бы приблизительно известна средняя величина изучаемого признака, то 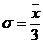 ;
;
4) при изучении альтернативного признака, если нет даже приблизительных сведений о доли единиц, обладающих заданным значением признака, берется максимально возможная величина дисперсии, равная 0,25.
|
|
|

МАЛАЯ ВЫБОРКА
Приведенные в вопросах 3 и 4 формулы средней ошибки выборки показывают; что ее величина зависит от объёма выборки (n), степени колеблемости изучаемого признака в генеральной совокупности (σ2) и способа отбора. Причем, чем меньше объем выборки, тем большую величину стандартной ошибки следует ожидать, а это в свою очередь снижает точность оценки параметров генеральной совокупности.
При выборках небольшого объема величина выборочной дисперсии используемой в качестве оценки дисперсии генеральной совокупности, может быть в значительной мере подвержена влиянию случайностей выборки. Поэтому при выборках небольшого объема методы оценки результатов выборочного наблюдения видоизменяются в сравнении с применяемыми в теории больших выборок.
Как правило, выборка считается малой, если обслёдуется не более 30 единиц: Таким образом, средняя ошибка малой выборки рассчитывается, по формуле:

В условиях малой выборки дисперсия выборочной совокупности не может рассматриваться в качестве оценки генеральной дисперсии.
Предельная ошибка выборки:
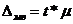 ,
,
где t – коэффициент доверия, который определяется по закону распределения Стьюдента, открытому в 1908 г. английским математиком У. Госсетом (псевдоним — Стьюдент).
|
|
|
Величина отношения Стьюдента t (краткие выдержки)
|
| Вероятность | ||
| 0,95 | 0,99 | 0,997 | |
| 4 | 2,776 | 4,604 | 6,435 |
| 9 | 2,262 | 3,250 | 4,024 |
| 14 | 2,145 | 2,977 | 3,583 |
| 20 | 2,086 | 2,845 | 3,376 |
| 24 | 2,064 | 2,797 | 3,302 |
| 28 | 2,048 | 2,763 | 3,250 |
Пример №4
Оздоровительный центр предлагает клиентам за короткий срок снижение веса до 10 кг. По результатам выборочного наблюдения 15 женщин выявлены следующие данные:
| № | Снижение веса, кг | № | Снижение веса, кг | № | Снижение веса, кг | № | Снижение веса, кг | № | Снижение веса, кг |
| 1 | 10,2 | 4 | 8,4 | 7 | 13,7 | 10 | 6,1 | 13 | 4,7 |
| 2 | 7,6 | 5 | 6,0 | 8 | 6,9 | 11 | 5,0 | 14 | 3,6 |
| 3 | 6,1 | 6 | 5,7 | 9 | 5,2 | 12 | 3,7 | 15 | 3,2 |
Определите в каких пределах находится генеральный параметр.
Выборочная средняя составляет 6,41 кг ( 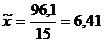 кг)( т е среднее снижение веса у обследованных женщин составило 6,41 кг.
кг)( т е среднее снижение веса у обследованных женщин составило 6,41 кг.
Выборочная дисперсия равна 7,061 (  )
)
Следовательно, средняя ошибка выборки составит 0,71 кг.
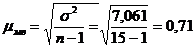 кг
кг
Оценим с вероятностью 0,99 предел возможных расхождений выборочной средней и генеральной средней. Так как число степеней свободы равно 14 (к = n-1= 15-1), то по таблице находим, что значение t, соответствующее вероятности 0,99, равно 2,977.
Тогда с вероятностью 0,99 можно предполагать, что ошибка выборочной средней будет не больше 2,114 кг (2,977 х 0,71), а снижение веса пациентов оздоровительного центра будет находиться в пределах от 4,3 до 8,52 кг (6,41 ±2,11). Следовательно, указанное в рекламе снижение веса на 10 кг имеет столь малую вероятность, что считается событием практически невозможным.
Дата добавления: 2018-05-02; просмотров: 1043; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 К=n-1
К=n-1