ПОНЯТИЕ И ПОКАЗАТЕЛИ ВАРИАЦИИ.
Вариация - это колеблемость значений признака в совокупности.
Показатели вариации
1 Размах вариации – разность между максимальным и минимальным значением признака в совокупности.
Недостаток – при расчете учитывают только крайние значения, вызванные аномальными причинами
2 Среднее линейное отклонение – средняя арифметическая из отклонение вариант от средней арифметической, взятое без учета знака этих отклонений.
Показывает, на сколько в среднем отклоняется значения изучаемого признака от средней арифметической.
Недостаток – использование модуля.
3 Дисперсия - квадрат стандартного отклонения. Этот показатель несет ту же информацию, что и стандартное отклонение, но труднее интерпретируется, поскольку единица измерения дисперсии представляют собой единицы измерения исходных данных, возведенных в квадрат.
s2= 
4 Среднее квадратическое отклонение - это положительный квадратный корень дисперсии. Оно определяется выборочным среднеквадратическим отклонением, которое представляет собой положительный квадратный корень выборочной дисперсии.
s = 
Показывает, на сколько в среднем отклоняется значения изучаемого признака от средней арифметической.
5 Коэффициент вариации - это отношение совокупного среднеквадратического отклонения к среднему значению
V= 
Если коэффициент вариации менее 33%, то совокупность считается однородной.
|
|
|
С помощью коэффициента вариации можно сравнить колеблемость одного и того же признака в разных совокупностях или вариации различных признаков в одной совокупности.
Рассчитаем показатели вариации – дисперсию, среднее линейное отклонение, среднее квадратическое отклонение (стандартное отклонение) и коэффициент вариации, используя данные задачи №3.
| Возраст, лет | Середина интервала (xi) | Число рабочих (f) | |xi-  |
| |xi- |*f
| |
| До 25 | 20 | 10 | |20-47,5|=27,5 |
| |
| 25-35 | 30 | 20 | 17,5 | 350 | |
| 35-45 | 40 | 50 | 7,5 | 375 | |
| 45-55 | 50 | 70 | 2,5 | 175 | |
| 55-65 | 60 | 30 | 12,5 | 375 | |
| Свыше 65 | 70 | 20 | 22,5 | 450 | |
| Итого | - | 200 | - | 2000 |
В среднем возраст работников отклоняется от среднего возраста 47,5 лет на 10 лет.
s2=
| Возраст, лет | Середина интервала (x) | Число рабочих (f) | (xi- )
| (xi- )2
| (xi- )2*f
|
| До 25 | 20 | 10 | -27,5 | 756,25 | 7562,5 |
| 25-35 | 30 | 20 | -17,5 | 306,25 | 6125,0 |
| 35-45 | 40 | 50 | -7,5 | 56,25 | 2812,5 |
| 45-55 | 50 | 70 | 2,5 | 6,25 | 437,5 |
| 55-65 | 60 | 30 | 12,5 | 156,25 | 4687,5 |
| Свыше 65 | 70 | 20 | 22,5 | 506,25 | 10125,0 |
| Итого | - | 200 | - | - | 31750,0 |
Тогда s2= 
=158,75
Среднее квадратическое отклонение: s = = 
=12,6.
Коэффициент вариации: V= 
=12,6/47,5*100=26,5%.
В среднем возраст работников отклоняется от среднего возраста 47,5 лет на 12,6 лет. Так как коэффициент вариации меньше 33%, то делаем вывод о статистической однородности совокупности. В противном случае необходимо разбивать совокупность на группы и все расчеты делать для каждой группы в отдельности.
|
|
|
По данным примера 6 темы «Сводка и группировка» оцените тесноту связи между изучаемыми признаками, рассчитав коэффициент детерминации эмпирическое корреляционное отношение.
Межгрупповая дисперсия вычисляется по формуле:
d2= 
, где:
– соответственно средняя i -й группы и общая средняя;
fi – объем i–й группы (межгруппавая дисперсия рассчитывается для результативного признака)
Для определения межгрупповой дисперсии произведем расчеты в таблице:
| Группы предприятий | Количество предприятий fi | Сумма затрат на перевозку, тыс. руб. в среднем на 1 предприятие, тыс. руб. Xi | 
| 
| 
|
| 15-32 | 9 | 701,1 | -299,2 | 89520,64 | 805685,76 |
| 32-49 | 6 | 1082,0 | 81,7 | 6674,89 | 40049,34 |
| 49-66 | 5 | 1440,8 | 440,5 | 194040,25 | 970201,25 |
| Итого | 20 | 1000,3 | - | - | 1815936,35 |
d2= 
Средняя из внутригрупповых дисперсии рассчитывается по формуле:
s2= 
где
s2i -внутригрупповая дисперсия i-й группы, которая рассчитывается отдельно для каждой группы:
Для 1 группы:
| Номера предприятий | Сумма затрат на перевозку, т. р.. | (Xi-  i) ;
i=701,1
| (Xi- i)2
|
| 5 | 472 | -229,1 | 52486,81 |
| 4 | 750 | 48,9 | 2391,21 |
| 6 | 840 | 138,9 | 19293,21 |
| 8 | 804 | 102,9 | 10588,41 |
| 10 | 724 | 22,9 | 524,41 |
| 11 | 579 | -122,1 | 14908,41 |
| 14 | 699 | -2,1 | 4,41 |
| 16 | 612 | -89,1 | 7938,81 |
| 18 | 830 | 128,9 | 16615,21 |
| Итого | 6310 | - | 124750,89 |
s21=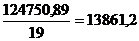 
|
|
|
Для 2 группы
| Номера предприятий | Сумма затрат на перевозку, т. р. | (Xi- i) ; i=1082
| (Xi- i)2
|
| 2 | 1080 | -2 | 4 |
| 3 | 1033 | -49 | 2401 |
| 9 | 1245 | 163 | 26569 |
| 13 | 1145 | 63 | 3969 |
| 15 | 889 | -193 | 37249 |
| 19 | 1100 | 18 | 324 |
| Итого | 6492 | - | 70516 |
s22= 
Для 3 группы
| Номера предприятий | Сумма затрат на перевозку, т. р. | (Xi- i) ; i=1440,8
| (Xi- i)2
|
| 1 | 1550 | 109,2 | 11924,64 |
| 7 | 1310 | -130,8 | 17108,64 |
| 12 | 1444 | 3,2 | 10,24 |
| 17 | 1500 | 59,2 | 3504,64 |
| 20 | 1400 | -40,8 | 1664,64 |
| Итого | 7204 | 34212,8 |
s23= 
Рассчитаем среднюю из внутригрупповых:
s2= 
=11474
По правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:
s2общ= d2+s2
s2общ=90796,8+11474=102270,8
Отношение межгрупповой дисперсии к общей называется коэффициентам детерминации:
h2= 
h2= 
=88,8%
Это означает, что вариация суммы затрат на перевозку на 89,4% зависит от грузооборота, а на 10,6% от остальных факторов.
|
|
|
Квадратный корень из коэффициента детерминации называется эмпирическое корреляционное отношение и характеризует силу связи между изучаемыми факторами:
h= 
h= 
=0,94
Согласно шкале связь между грузооборотом и суммой затрат весьма высокая.
Тема 5 «Ряды динамики»
Дата добавления: 2018-05-02; просмотров: 409; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!