СВОЙСТВА СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ. РАСЧЁТ СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ СПОСОБОМ «МОМЕНТОВ».
Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.
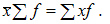
2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:
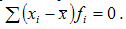
4.Сумма квадратов отклонений вариантов от средней меньше, чем сумма квадратов отклонений от любой другой произвольной величины 
, т.е:
5. Если все варианты ряда уменьшить или увеличить на одно и то же число , то средняя уменьшится на это же число :
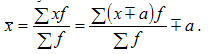
6.Если все варианты ряда уменьшить или увеличить в 
раз, то средняя также уменьшится или увеличится в раз:
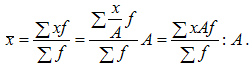
7.Если все частоты (веса) увеличить или уменьшить в 
раз, то средняя арифметическая не изменится:
Этот способ основан на использовании математических свойств средней арифметической величины. В этом случае средняя величина вычисляется по формуле: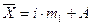 
, где i – величина равного интервала или любое постоянное число не равное 0; m1 – момент первого порядка, который рассчитывается по формуле: 
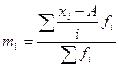; А – любое постоянное число.
18 СРЕДНЯЯ ГАРМОНИЧЕСКАЯ ПРОСТАЯ И ВЗВЕШЕННАЯ.
Средняя гармоническая используется в случаях, кода неизвестны частоты (fi), а известен объем изучаемого признака (xi*fi=Mi).
|
|
|
По примеру 2 определим среднюю заработную плату в 2001г.
В исходной информации 2001г. нет данных о количестве работников, однако ее нетрудно рассчитать как отношение фонда оплаты труда к средней зарплате.
Тогда 
2769,4 руб., т.е. средняя зарплата в 2001г. –2769,4 руб.
В данном случае использована средняя гармоническая: 
,
где Мi –фонд оплаты труда в отдельном цеху; xi –зарплата в отдельном цеху.
Следовательно, средняя гармоническая применяется тогда, когда неизвестен один из сомножителей, но известно произведение «М».
Средняя гармоническая используется для расчета средней производительности труда, среднего процента выполнения норм, средней зарплаты и т.д.
Если произведения «М» равны между собой, то используется средняя гармоническая простая: 
, где n – число вариант.
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ И СРЕДНЯЯ ХРОНОЛОГИЧЕСКАЯ.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня ряда к предыдущему уровню.
|
|
|
, 
- цепные коэффициенты роста;
n – число цепных коэффициентов роста.
Если исходные данные даны по состоянию на определенные даты, то средний уровень признака определяется по формуле средней хронологической. Если промежутками между датами (моментами) равные, то средний уровень определяется по формуле средней хронологической простой..
Рассмотрим ее расчет на конкретных примерах.
Пример. Имеются следующие данные об остатках вкладов населения в банках России в первом полугодии 1997 г. (на начало месяца):
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Сумма вкладов у, трлн руб. | 127,6 | 129,7 | 132,7 | 133,8 | 135,4 | 137,1 | 139,8 |
Средний остаток вкладов населения за первое полугодие 1997 г. (по формуле средней хронологической простой) составил:
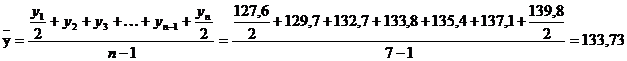трлн руб.
n – число дат.
В случае неравных промежутков между датами среднюю хронологическую можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами.
,
- средний уровень изучаемого признака в i-том периоде;
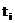- продолжительность i-того периода.
Пример. Пусть имеются следующие данные о наличии товарных остатков на складе за 1997 г.:
| Дата учета | 01.01.97 | 01.03.97 | 01.06.97 | 01.11.97 | 01.01.98 |
| Остатки товаров у, тыс. руб. | 126 | 130 | 138 | 150 | 160 |
|
|
|
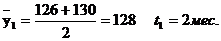
тыс. руб.
Дата добавления: 2018-05-02; просмотров: 603; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!