Тема 4 «Средние величины и вариация»
ПОНЯТИЕ СРЕДНИХ ВЕЛИЧИН. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ СРЕДНИХ ВЕЛИЧИН.
Средняя величина - показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.
Если индивидуальные значения признака заменить средней величиной, то общий объем признака не измениться
Основные положения теории средних величин.
1. Индивидуальные значения, из которых исчисляются средние, должны относится к однородной совокупности, а число их должно быть значительным.
2. Метод средних величин должен сочетаться с методом группировок.
3. Необходимо рассчитывать внутригрупповые средние.
В статистике используют различные виды средних величин. Выбор той или иной средней зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ПРОСТАЯ И ВЗВЕШЕННАЯ.
Средняя арифметическая используется для определения среднего уровня изучаемого признака, когда исходные данные представлены рядом распределения.
Средняя арифметическая простая используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое или частоты ряда распределения равны между собой.
Пример № 1
Найти среднюю выработку рабочих бригады, если известны следующие данные о выработке:
|
|
|
| Табельный номер рабочего | 001 | 002 | 003 | 004 | 005 |
| Выработка, шт/час (xi) | 135 | 141 | 153 | 159 | 162 |
,
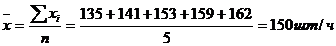где n – число вариант.
Средняя арифметическая взвешенная применяется при расчете средних величин, значения которых могут повторяться, поэтому расчет средней величины производится по сгруппированным данным (т.е. если частоты не равны между собой).
Пример 2
Определите среднюю заработную плату в 2000г.
| Цех | 2000г. | 2001г. | ||
| Заработная плата в среднем по цеху, руб. (x) | Число рабочих, чел. (f) | Заработная плата в среднем по цеху, руб. (x) | Фонд оплаты труда, руб. (M) | |
| №1 | 2500 | 100 | 2200 | 198000 |
| №2 | 2000 | 120 | 2700 | 351000 |
| №3 | 3000 | 150 | 3200 | 448000 |
| Итого | - | 370 | - | 997000 |
: 
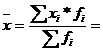
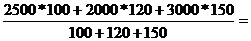2540,5 руб.
Следовательно, средняя заработная плата в 2000г. по всей совокупности работников составляла 2540,5 руб.
Частные случаи расчета средней арифметической
1. Средняя арифметическая интервального ряда распределения.
Пример 3
| Возраст, лет | До 25 | 25-35 | 35-45 | 45-55 | 55-65 | Свыше 65 |
| Число рабочих | 10 | 20 | 50 | 70 | 30 | 20 |
Определить средний возраст рабочих.
Для преобразования непрерывного ряда в дискретный определим середины каждого интервала. При этом величина каждого открытого интервала приравнивается к величине смежного интервала.
|
|
|
| Возраст, лет (открытые интервалы) | Возраст, лет (закрытые интервалы) | Середина интервала (xi) | Число рабочих (fi) | xi*fi | Накопленная частота |
| До 25 | 15-25 | 20 | 10 | 200 | 10 |
| 25-35 | 25-35 | 30 | 20 | 600 | 10+20=30 |
| 35-45 | 35-45 | 40 | 50 | 2000 | 10+20+50=80 |
| 45-55 | 45-55 | 50 | 70 | 3500 | 150 |
| 55-65 | 55-65 | 60 | 30 | 1800 | 180 |
| Свыше 65 | 65-75 | 70 | 20 | 1400 | 200 |
| Итого | - | - | 200 | 9500 | - |
Вычислим среднюю по формуле средней арифметической взвешенной: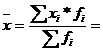 
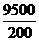=47,5 лет. Таким образом, средний возраст рабочих – 47,5 лет.
2. Средняя арифметическая из относительных величин.
В данном случае за варианты принимают сами относительные величины, за частоты – основание относительной величины.
3. Средняя арифметическая из групповых средних величин
В данном случае за варианты принимают групповые средние величины, за частоты – численность групп.
Дата добавления: 2018-05-02; просмотров: 583; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!