Застосування теореми Банаха до розв’язання нелінійних інтегральних рівнянь Гамерштейна
Це рівняння виду 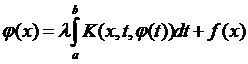 . Очевидно, що це рівняння є складнішим за рівняння Фредгольма, бо невідома функція входить в ядро. Будемо вважати, що
. Очевидно, що це рівняння є складнішим за рівняння Фредгольма, бо невідома функція входить в ядро. Будемо вважати, що 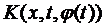 – неперервна, як функція трьох змінних
– неперервна, як функція трьох змінних 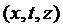 і задовольняє по z умову Ліпшиця:
і задовольняє по z умову Ліпшиця:
 ,
, 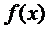 – неперервна. Розглянемо оператор
– неперервна. Розглянемо оператор  ,
, 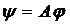 .
.
Перевіримо виконання умов теореми Банаха:
1. С[a,b] – повний.
2. Відображення в себе.
3. Стиск:

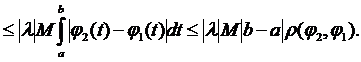
Нерівність справедлива при всіх x, отже виконується і для максимального, 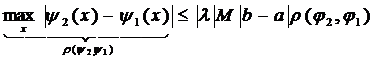 . Щоб виконувалась умова стиску вимагатимемо
. Щоб виконувалась умова стиску вимагатимемо 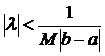 . Отже вихідне інтегральне рівняння Гамерштейна має єдиний розв’язок.
. Отже вихідне інтегральне рівняння Гамерштейна має єдиний розв’язок.
Застосування теореми Банаха до розв’язування інтегральних рівнянь Вольтера.
Інтегральним рівнянням Вольтера зветься рівняння виду: 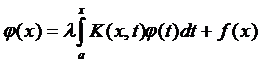 . Усі вимоги накладаємо на функції так як і в попередніх рівняннях. Покажемо, що метод послідовних наближень застосований для всіх x. Покажемо, що умови стиску виконуються завжди для n-того наближення при
. Усі вимоги накладаємо на функції так як і в попередніх рівняннях. Покажемо, що метод послідовних наближень застосований для всіх x. Покажемо, що умови стиску виконуються завжди для n-того наближення при 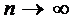 .
.
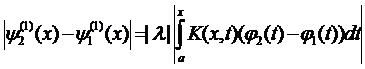
 ,
,  ;
;
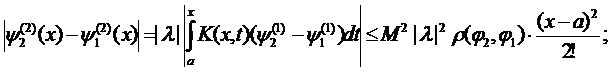
……………………………………………………………….
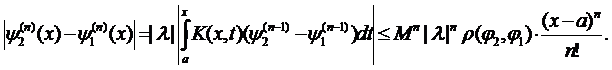
Зафіксувавши x=b матимемо:
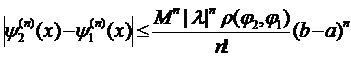 . Завжди можна підібрати n, так щоб
. Завжди можна підібрати n, так щоб 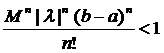 .
.
Контрольні запитання.
1. Дати означення стискаючого відображення і довести його неперервність.
2. Сформулювати та довести теорему Банаха. Дати їй геометричне тлумачення.
3. Довести теорему існування і єдиності розв’язку задачі Коші для диференціального рівняння 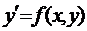 , f(x
, f(x 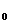 )=y
)=y 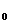 .
.
4. Дати означення нормальної системи диференціальних рівнянь.
5. Сформулювати теорему про існування і єдиність розв’язку задачі Коші для нормальної системи диференціальних рівнянь, вказати схему її доведення.
|
|
|
6. За допомогою теореми Банаха вияснити за яких умов існує єдиний розв’язок інтегрального рівняння Фредгольма.
7. Сформулювати теорему існування і єдиності розв’язку нелінійного інтегрального рівняння та рівняння Вольтера.
Вправи.
1. За допомогою теореми Банаха знайти кілька наближень розв’язку рівняння 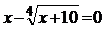 на відрізку [1,2].
на відрізку [1,2].
2. Оператор А заданий співвідношеннями
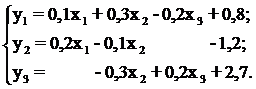
Перевірити виконання умов теореми Банаха в просторі  .
.
3. Як оцінити похибку між n-тим наближенням xn розв’язку рівняння 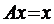 та точним значенням х.
та точним значенням х.
4. Знайти кілька наближень розв’язку задачі Коші  , y(0)=1, і оцінити величину відрізка на якому розв’язок існує і єдиний.
, y(0)=1, і оцінити величину відрізка на якому розв’язок існує і єдиний.
Розв’язання.
1. Сегмент [1;2] є повний простір як замкнений підпростір повного простору. Покажемо, що y= 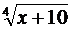 є відображення в себе, тобто його значення не виходять за межі сегмента [1;2]. Маємо f(1)=
є відображення в себе, тобто його значення не виходять за межі сегмента [1;2]. Маємо f(1)= 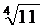 >1, f(2)=
>1, f(2)= 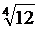 <2. Крім того
<2. Крім того 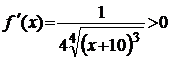 , тобто функція монотонна, і, таким чином, найбільше і найменше значення функція досягає на кінцях сегменту. Маємо, що похідна
, тобто функція монотонна, і, таким чином, найбільше і найменше значення функція досягає на кінцях сегменту. Маємо, що похідна 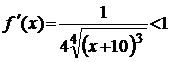 для
для  x
x  [1,2], тобто виконується умова стиску. Таким чином виконуються всі три умови теореми Банаха і можемо знаходити наближене значення кореня рівняння методом послідовних наближень. Наприклад покладемо x
[1,2], тобто виконується умова стиску. Таким чином виконуються всі три умови теореми Банаха і можемо знаходити наближене значення кореня рівняння методом послідовних наближень. Наприклад покладемо x 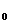 =1. Тоді x
=1. Тоді x  =
= 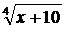 =
= 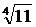 , x
, x 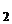 =
= 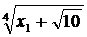 =
=  ...
...
|
|
|
2. По-перше, простір R 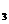 – повний. По-друге, маємо відображення в себе. Перевіримо виконання умов стиску:
– повний. По-друге, маємо відображення в себе. Перевіримо виконання умов стиску:
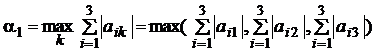 , де
, де  – сума модулів коефіцієнтів при хj, які відповідно рівні 0,3; 0,7; 0,4. Оскільки найбільша з сум рівна 0,7, то
– сума модулів коефіцієнтів при хj, які відповідно рівні 0,3; 0,7; 0,4. Оскільки найбільша з сум рівна 0,7, то 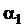 =0,7<1 i умова стиску виконується.
=0,7<1 i умова стиску виконується.
3. В процесі доведення теореми Банаха, зокрема, при доведенні фундаментальності послідовності {xn}, одержується оцінка  (xn,xm)
(xn,xm) 
 (x0,x1), де
(x0,x1), де 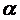 –константа, яка фігурує в умові стиску. Перейдемо в нерівності до границі, коли m прямує до нескінченності. Дістанемо шукану оцінку:
–константа, яка фігурує в умові стиску. Перейдемо в нерівності до границі, коли m прямує до нескінченності. Дістанемо шукану оцінку:  (xn,xm)
(xn,xm) 
 (x0,x1).
(x0,x1).
4. Диференціальне рівняння 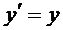 разом з початковою умовою y(0)=1, еквівалентне наступному інтегральному рівнянню y(x)=1+
разом з початковою умовою y(0)=1, еквівалентне наступному інтегральному рівнянню y(x)=1+ 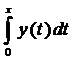 . Покладемо y0=1, тоді отримаємо: y1=1+
. Покладемо y0=1, тоді отримаємо: y1=1+ 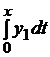 =1+x; y2=1+
=1+x; y2=1+ 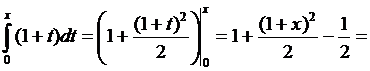 1+x+
1+x+ 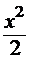 ;...
;...
Помічаємо, що послідовні наближення співпадають з частковими сумами ряду Тейлора для функції еx. Зауважимо, як випливає з теореми Банаха, існування і єдиність розв’язку буде забезпечена в прямокутнику з центром в точці (0,1),  .
.
Задачі.
1. Вказати достатні умови, які забезпечують існування і єдиний корінь рівняння F(x)=0.
2. Показати, що коли функція f(x) однієї змінної має похідну 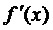 , причому
, причому 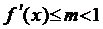 , то відображення y=f(x) буде стискаючим.
, то відображення y=f(x) буде стискаючим.
|
|
|
3. За допомогою теореми Банаха знайти кілька наближених розв’язків рівнянь:
а) x3+x–20=0;
б) x= 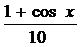 , [0,1];
, [0,1];
в) x=(x+1);
г) x=1– 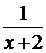 , [0,4];
, [0,4];
д) x=x3–2, [1,2];
е) x=1+ 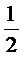 arctg x;
arctg x;
є) x= 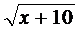 , [0,1];
, [0,1];
ж) x2=sin x;
з) x2=ln(x+1);
і) x3=ex+2.
4. Вказати умови стиску у просторах  для розв’язання системи n рівнянь з n невідомими виду:
для розв’язання системи n рівнянь з n невідомими виду:

5. Дано рівняння: a) 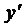 =x–y
=x–y 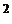 , y(0)=0;
, y(0)=0;
б) 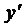 =x
=x 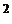 +y
+y 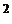 , y(0)=1;
, y(0)=1;
в) 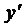 =xy, y(0)=1;
=xy, y(0)=1;
г) 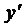 =y
=y 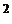 +xy+x
+xy+x 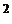 , y(0)=1.
, y(0)=1.
Знайти кілька наближених розв’язків даних рівнянь і оцінити величину відрізка на якому розв’язок існує і єдиний.
КОМПАКТИ
Наведемо приклад простору, для якого не виконується теорема Больцано-Вейєрштрасса, а саме: з усякої обмеженої числової послідовності можна виділити збіжну підпослідовність. Ця теорема не справедлива в довільному метричному просторі. Розглянемо простір l2: 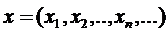 ,
, 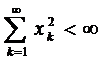 . Розглянемо в цьому просторі послідовність:
. Розглянемо в цьому просторі послідовність:
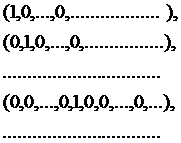
Ця послідовність буде обмеженою, бо всі її члени знаходяться в середині абстрактної кулі з центром в точці 0 і 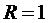 . Дійсно:
. Дійсно:
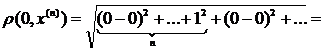 1. Очевидно, що з такої послідовності не можна виділити збіжну підпослідовність, бо якби це було б можливо, то отримана послідовність була б фундаментальною. Але
1. Очевидно, що з такої послідовності не можна виділити збіжну підпослідовність, бо якби це було б можливо, то отримана послідовність була б фундаментальною. Але 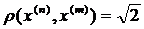 (не прямує до нуля). Виділимо клас множин, для яких виконується теорема Больцано-Вейєрштрасса. Це приводить до поняття компактності.
(не прямує до нуля). Виділимо клас множин, для яких виконується теорема Больцано-Вейєрштрасса. Це приводить до поняття компактності.
|
|
|
Означення. Нехай маємо метричний простір 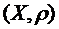 і множину
і множину 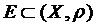 . Множина
. Множина 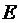 називається компактною (компактом), якщо із будь-якої послідовності цієї множини можна виділити збіжну підпослідовність, границя якої належить множині
називається компактною (компактом), якщо із будь-якої послідовності цієї множини можна виділити збіжну підпослідовність, границя якої належить множині 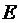 .
.
Означення. Множина 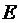 зветься компактом, якщо із будь-якого її нескінченого покриття системою відкритих множин можна виділити скінчене підпокриття.
зветься компактом, якщо із будь-якого її нескінченого покриття системою відкритих множин можна виділити скінчене підпокриття.
Приклади компактів.
1. Сегмент 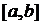 – компакт.
– компакт.
2. Інтервал 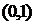 – не є компактом.
– не є компактом.
Теорема. Усякий компакт є множина замкнена і обмежена.
Доведення. Замкненість. Нехай x – гранична точка 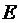 . Доведемо, що вона належить
. Доведемо, що вона належить 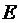 . Розглянемо систему абстрактних куль
. Розглянемо систему абстрактних куль 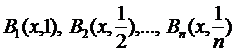 ,… з центром в точці x і радіусами
,… з центром в точці x і радіусами 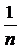 . Тоді виберемо з кожної кулі по представнику
. Тоді виберемо з кожної кулі по представнику 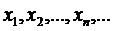 .
. 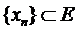 ;
;  ;
;  при
при  . Отже і будь-яка підпослідовність теж прямує до x. І за означенням компакту належатиме E, а це і доводить замкненість.
. Отже і будь-яка підпослідовність теж прямує до x. І за означенням компакту належатиме E, а це і доводить замкненість.
Обмеженість. Нехай компакт E є множина необмежена. Візьмемо довільну кулю  , де x0 – довільна точка компакту, r– довільне число. В силу необмеженості буде існувати точка x1, яка не належить кулі
, де x0 – довільна точка компакту, r– довільне число. В силу необмеженості буде існувати точка x1, яка не належить кулі 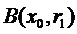 з радіусом
з радіусом 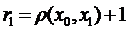 . В силу необмеженості буде існувати точка x2, яка не належить кулі
. В силу необмеженості буде існувати точка x2, яка не належить кулі  з радіусом
з радіусом  . Продовжуючи цей процес отримаємо послідовність елементів:
. Продовжуючи цей процес отримаємо послідовність елементів: 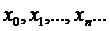 . Ця послідовність не буде фундаментальною, бо відстань між будь-якими її елементами буде більшою 1. Тим більше, будь-яка підпослідовність теж не буде фундаментальною, а це суперечить тому, що Е – компакт.
. Ця послідовність не буде фундаментальною, бо відстань між будь-якими її елементами буде більшою 1. Тим більше, будь-яка підпослідовність теж не буде фундаментальною, а це суперечить тому, що Е – компакт.
Теорему доведено.
Компакти в Rm.
Компакти в Rm можна описати теоремою.
Теорема. Для того, щоб множина E 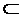 Rm була компактною, необхідно і достатньо, щоб вона була замкненою і обмеженою.
Rm була компактною, необхідно і достатньо, щоб вона була замкненою і обмеженою.
Доведення. Необхідність. Дано E – компакт, тоді з попередньої теореми множина замкнена і обмежена.
Достатність. Нехай E – замкнена і обмежена. Доведемо, що E – компакт. Розглянемо довільну послідовність  . Вона буде обмеженою в тому розумінні, що всі її точки будуть знаходитись в кулі з центром в довільній точці x і скінченним радіусом R. За теоремою Больцано-Вейєрштрасса з послідовності
. Вона буде обмеженою в тому розумінні, що всі її точки будуть знаходитись в кулі з центром в довільній точці x і скінченним радіусом R. За теоремою Больцано-Вейєрштрасса з послідовності 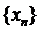 можна виділити збіжну підпослідовність. Нехай
можна виділити збіжну підпослідовність. Нехай 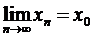 . Покажемо, що x0
. Покажемо, що x0 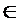 E. Так як x0 – гранична точка, тоді в силу замкненості x0
E. Так як x0 – гранична точка, тоді в силу замкненості x0 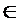 E.
E.
Теорему доведено.
Дата добавления: 2018-04-15; просмотров: 649; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
