ЛІНІЙНІ ОПЕРАТОРИ І ЛІНІЙНІ ФУНКЦІОНАЛИ
Нехай є два лінійних простори  і
і  . Якщо кожному елементу x простору
. Якщо кожному елементу x простору  поставлено у відповідність цілком певний елемент y із простору
поставлено у відповідність цілком певний елемент y із простору  , то кажуть, що заданий оператор
, то кажуть, що заданий оператор  , який діє у просторі
, який діє у просторі  із значеннями в
із значеннями в  .
.
Означення. Оператор A називається лінійним, якщо для  і для будь-яких чисел α1 і α2 виконується рівність
і для будь-яких чисел α1 і α2 виконується рівність 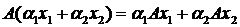 .
.
Приклад.
 .
.
Оператор діє в просторі  . Будемо вважати, що K і φ – неперервні. Перевіримо умову лінійності:
. Будемо вважати, що K і φ – неперервні. Перевіримо умову лінійності:

З лінійності оператора випливають властивості:
1. 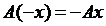 ;
;
2.  .
.
Означення. Лінійний оператор  називається неперервним в точці x0, якщо із збіжності будь-якої послідовності
називається неперервним в точці x0, якщо із збіжності будь-якої послідовності  випливає, що відповідна послідовність значень оператора
випливає, що відповідна послідовність значень оператора  .Тут збіжність розуміється за нормою даного простору, тобто якщо при
.Тут збіжність розуміється за нормою даного простору, тобто якщо при 
 , то
, то  .
.
Теорема. Якщо лінійний оператор неперервний в точці x0, то він неперервний і в довільній точці довільного простору.
Доведення. Розглянемо довільну послідовність  і покажемо, що
і покажемо, що  . Розглянемо довільний елемент
. Розглянемо довільний елемент 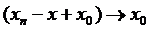 . Тоді в силу неперервності в x0
. Тоді в силу неперервності в x0  . Використаємо лінійність:
. Використаємо лінійність:  , тоді
, тоді 
 (при
(при  ).
).
Означення. Лінійний оператор, який діє в лінійному просторі  із значеннями в лінійному просторі
із значеннями в лінійному просторі  називається обмеженим, якщо існує таке число
називається обмеженим, якщо існує таке число  , що для
, що для  .
.
Теорема. Для того, щоб лінійний оператор був неперервним у будь-якій точці x, необхідно і достатньо, щоб він був обмеженим.
Доведення. Необхідність. Дано:  – неперервний оператор. Доведемо обмеженість, тобто що
– неперервний оператор. Доведемо обмеженість, тобто що  ,
, 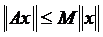 . Припустимо протилежне, що оператор необмежений. Це означає, що для
. Припустимо протилежне, що оператор необмежений. Це означає, що для 
 .
.
|
|
|
Розглянемо елемент  і оцінимо за нормою:
і оцінимо за нормою:
 ,
, 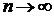 ;
;  ,
, 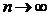 ,
,  . Тоді, в силу неперервності,
. Тоді, в силу неперервності,  .
.
З іншого боку  , не прямує до нуля,
, не прямує до нуля,  . Отримали суперечність.
. Отримали суперечність.
Достатність. Дано, що оператор обмежений, тобто  ,
, 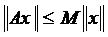 . Доведемо, що для
. Доведемо, що для  ,
, 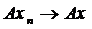 .
.
 ;
;  .
.
Теорему доведено.
Норма оператора.
Нехай маємо лінійний обмежений оператор:  ,
,  .
.
Означення. Найменша з компонент  , яка фігурує в умові обмеженості зветься нормою оператора A і позначається
, яка фігурує в умові обмеженості зветься нормою оператора A і позначається 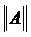 ,
,  .
.
По-іншому, число  зветься нормою оператора, якщо для
зветься нормою оператора, якщо для  ,
,  ,
, 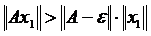 .
.
Приклад. Маємо відображення 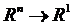 ,
,
 .
.
 – фіксований вектор.
– фіксований вектор.
 – змінний вектор.
– змінний вектор.
Знайдемо норму оператора
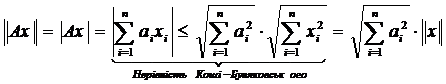 ,
,
 .
.
Покажемо, що насправді  рівна правій частині. Для цього достатньо знайти елемент x, щоб нерівність перетворювалася б в рівність. Розглянемо елемент
рівна правій частині. Для цього достатньо знайти елемент x, щоб нерівність перетворювалася б в рівність. Розглянемо елемент  , тоді:
, тоді:
 .
.
Контрольні запитання.
1. Дати означення лінійного оператора.
2. Дати означення неперервності лінійного оператора.
3. Який оператор називається обмеженим?
4. Що називається нормою оператора?
5. Дати означення лінійного функціоналу. Навести приклади.
6. Який загальний вигляд лінійних функціоналів у просторах  і
і 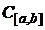 ?
?
7. Який оператор називається оборотним?
|
|
|
Вправи.
1. Розглянемо у просторі неперервних функцій на відрізку  оператор, який визначається формулою
оператор, який визначається формулою  де
де  – деяка фіксована неперервна функція двох змінних. Довести лінійність даного оператора.
– деяка фіксована неперервна функція двох змінних. Довести лінійність даного оператора.
2. Показати, що оператор диференціювання 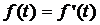 , який діє в підпросторі неперервних функцій, є лінійним, але не неперервним.
, який діє в підпросторі неперервних функцій, є лінійним, але не неперервним.
3. Довести, що в просторі Rn будь-який лінійний функціонал може бути поданий за формулою  , де
, де  цілком певний вектор, а
цілком певний вектор, а  – довільний вектор.
– довільний вектор.
4. Знайти норму оператора, який діє з простору Rn в просторі R1 і який визначається рівністю 
Розв’язання.
1. Маємо: 
 , що й доводить лінійність оператора.
, що й доводить лінійність оператора.
2. Лінійність даного оператора очевидна. Той факт, що даний оператор не є неперервним випливає, наприклад, з того, що послідовність  збігається до нуля (в метриці
збігається до нуля (в метриці  ), а послідовність
), а послідовність  ні.
ні.
3. Подамо x через одиничні вектори 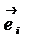 за формулою
за формулою  . Тоді, використавши лінійність функціонала, дістанемо
. Тоді, використавши лінійність функціонала, дістанемо
 , що й треба було довести.
, що й треба було довести.
4. Маємо, що  . За означенням норми оператора виходить, що
. За означенням норми оператора виходить, що  . Розглянемо елемент
. Розглянемо елемент  . Оскільки
. Оскільки  , то
, то 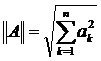 .
.
Задачі.
1. Довести, що коли лінійний оператор А неперервний в одній точці x  лінійного нормованого простору R, то він неперервний в R.
лінійного нормованого простору R, то він неперервний в R.
|
|
|
2. Довести, що будь-який обмежений лінійний оператор є неперервним.
3. Встановити загальний вигляд лінійного функціонала в просторі l  .
.
4. Дано функціонали
–  – фіксована точка із сегмента
– фіксована точка із сегмента 
– 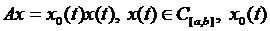 – фіксована точка із сегмента
– фіксована точка із сегмента 
– 
– 
Дослідити дані функціонали на лінійність, обмеженість і знайти їх норми.
5. Чи буде лінійним оператор  ?
?
6. Чи буде лінійним оператор  ? Чи буде він неперервним оператором з
? Чи буде він неперервним оператором з  в
в  ?
?
ЛІНІЙНІ ДОДАТНІ ОПЕРАТОРИ
В теорії наближень функції, фундаментальну роль відіграє теорема Вейєрштрасса, про те, що будь-яку неперервну функцію  на сегменті
на сегменті  можна як завгодно точно наблизити алгебраїчним многочленом.
можна як завгодно точно наблизити алгебраїчним многочленом.
Якщо функція достатньо гладка (має багато похідних) і залишковий член формули Тейлора прямує до нуля, то теорема Вейєрштрасса очевидна. В ролі многочлена в цьому випадку виступатиме многочлен Тейлора.
Однак функція може мати похідні всіх порядків, і її не можна наблизити многочленом Тейлора.
Крім того можна уявити функцію, яка є неперервною і немає похідну в жодній точці. Виявляється, що й таку функцію можна наблизити алгебраїчним многочленом. Доведемо теорему Вейєрштрасса за допомогою лінійних додатних операторів.
|
|
|
Розглянемо лінійний оператор  , який заданий у просторі неперервних функцій
, який заданий у просторі неперервних функцій  , так, що він залежить від функції
, так, що він залежить від функції  і від x. Прикладом такого оператора можуть бути многочлени Бернштейна
і від x. Прикладом такого оператора можуть бути многочлени Бернштейна  .
.
Означення. Лінійний оператор  зветься додатним, якщо він кожній невід’ємній функції
зветься додатним, якщо він кожній невід’ємній функції  ставить у відповідність невід’ємне значення оператора. Оператор Бернштейна буде таким оператором для функцій
ставить у відповідність невід’ємне значення оператора. Оператор Бернштейна буде таким оператором для функцій  , які задані на
, які задані на  .
.
Ясно, що коли  , то
, то  . Справді,
. Справді,  , тоді
, тоді 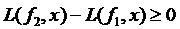 ,
,  .
.
Теорема (Коровкіна). Нехай маємо послідовність лінійних додатних операторів 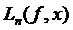 , які задані в просторі неперервних функцій
, які задані в просторі неперервних функцій 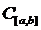 і виконуються умови:
і виконуються умови:
1.  ,
,
2.  ,
,
3.  ,
,
де 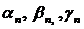 – нескінченно малі, які рівномірно по всіх x прямують до нуля, при
– нескінченно малі, які рівномірно по всіх x прямують до нуля, при 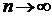 . Тоді послідовність лінійних операторів рівномірно прямує до неперервної функції
. Тоді послідовність лінійних операторів рівномірно прямує до неперервної функції  .
.
Доведення. Оскільки  неперервна на
неперервна на  , то за першою теоремою Вейєрштрасса вона буде обмежена, тобто:
, то за першою теоремою Вейєрштрасса вона буде обмежена, тобто:
 ,
,
 . (1)
. (1)
За теоремою Кантора функція  буде рівномірно неперервна на
буде рівномірно неперервна на  . Це означає, що для
. Це означає, що для  ,
,  ,
, 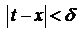 :
:

 . (2)
. (2)
З нерівностей (1) і (2) випливає така нерівність:
 . (3)
. (3)
Потрібно проаналізувати два випадки, коли  і
і  . Подіємо на нерівність (3) оператором і врахуємо, що він додатній і лінійний.
. Подіємо на нерівність (3) оператором і врахуємо, що він додатній і лінійний.
 (4)
(4)
Маємо: 
 ,
,
при  .
.
Тоді нерівність (4) набуває вигляду :
 .
.
При досить великому натуральному M, ми можемо досягти того, що буде виконуватися нерівність:

А це і доводить, що послідовність лінійних додатних операторів прямує до  рівномірно (бо нерівність виконується для всіх x).
рівномірно (бо нерівність виконується для всіх x).
Теорема доведена.
Теорема Бернштейна. Нехай маємо функцію  , яка неперервна на сегменті
, яка неперервна на сегменті  . Тоді многочлени Бернштейна
. Тоді многочлени Бернштейна  прямують до
прямують до  рівномірно.
рівномірно.
Доведення. Для доведення достатньо переконатись, що для многочленів Бернштейна виконуються умови теореми Коровкіна.
Справді, даний оператор додатний і лінійний. Крім того маємо:
1.  ,
, 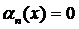 . Перша умова виконується.
. Перша умова виконується.
2.  ,
,
 .
.
Будемо мати:
 ,
,  .
.
3.  ,
,



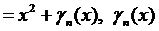 – нескінченно мала.
– нескінченно мала.
Всі умови теореми Коровкіна виконуються. Отже, многочлени Бернштейна рівномірно прямують до функції  , яка задана на
, яка задана на  .
.
Теорема Вейєрштрасса. Для будь-якої функції  неперервної на довільному сегменті
неперервної на довільному сегменті  існує послідовність алгебраїчних многочленів
існує послідовність алгебраїчних многочленів  , які рівномірно прямують до функції
, які рівномірно прямують до функції  .
.
Доведення. Зробимо заміну  , якщо
, якщо  , y=0,
, y=0,
 , y=1.
, y=1.
Тоді функція  задана на сегменті
задана на сегменті  . Цю функцію
. Цю функцію  , яка вже задана на
, яка вже задана на  , ми можемо як завгодно точно наблизити многочленом Бернштейна
, ми можемо як завгодно точно наблизити многочленом Бернштейна  :
:
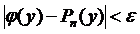 .
.
Повертаємось до старої змінної x:  . В результаті цієї заміни функція
. В результаті цієї заміни функція  перетвориться в
перетвориться в  , x
, x 
 , а
, а  буде алгебраїчним многочленом
буде алгебраїчним многочленом  . Матимемо, що
. Матимемо, що  .
.
Теорема доведена.
Контрольні запитання.
1. Який оператор на просторі неперервних функцій називається додатнім?
2. Довести лінійність й додатність операторів Бернштейна і Валле-Пуассона.
3. Довести теорему Коровкіна про збіжність послідовності лінійних додатніх операторів до неперервної функції  .
.
4. Довести теорему Бернштейна.
5. Довести теорему Вейєрштрасса про збіжність послідовності алгебраїчних многочленів до неперервної на відрізку  функції
функції  .
.
КОНТРОЛЬНА РОБОТА
Зразок контрольної роботи.
1.  . Довести, що дане відображення стискаюче. Однак рівняння
. Довести, що дане відображення стискаюче. Однак рівняння  не має дійсних коренів. Чому?
не має дійсних коренів. Чому?
2. Довести, що замкнений одиничний квадрат є компакт.
3. У просторі  норму елемента введено за формулою
норму елемента введено за формулою  . Перевірити виконання аксіоми норми.
. Перевірити виконання аксіоми норми.
4. Знайти норму функціонала 
5. За допомогою леми Гейне-Бореля довести першу теорему Больцано-Коші.
Розв’язання.
1. Дане відображення не є відображенням в себе. (Чому?). Отже, не виконується одна з умов теореми Банаха.
2. За теоремою Больцано-Вейєрштрасса з обмеженої послідовності у просторі  можна виділити збіжну підпослідовність. В силу замкненості одиничного квадрата границя підпослідовності належатиме даному квадрату.
можна виділити збіжну підпослідовність. В силу замкненості одиничного квадрата границя підпослідовності належатиме даному квадрату.
3. Маємо:
a).  , причому
, причому  тоді і тільки тоді, коли всі координати вектора
тоді і тільки тоді, коли всі координати вектора  рівні нулеві;
рівні нулеві;
b).  ;
;
c).  .
.
Дана нерівність виконується при всіх i, зокрема й тоді, коли в лівій частині стоїть максимум з усіх і, тобто  .
.
4. 

 . Отже,
. Отже, 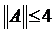 . Взявши тепер в якості функції
. Взявши тепер в якості функції  дещо згладжену функцію
дещо згладжену функцію  , переконаємось, що насправді
, переконаємось, що насправді  .
.
5. Припустимо, міркуючи від супротивного, що в жодній точці сегмента  функція
функція  не перетворюється в нуль, тобто зберігає знак у всіх внутрішніх точках сегмента
не перетворюється в нуль, тобто зберігає знак у всіх внутрішніх точках сегмента  . В силу неперервності функція
. В силу неперервності функція  зберігатиме знак і в деякому околі точки x. Ця система околів утворює нескінченне відкрите покриття сегмента
зберігатиме знак і в деякому околі точки x. Ця система околів утворює нескінченне відкрите покриття сегмента  . За лемою Гейне-Бореля з даного нескінченного покриття можна виділити скінченне підпокриття, в кожному з інтервалів якого функція зберігає знак. А це суперечить тому, що на кінцях сегмента
. За лемою Гейне-Бореля з даного нескінченного покриття можна виділити скінченне підпокриття, в кожному з інтервалів якого функція зберігає знак. А це суперечить тому, що на кінцях сегмента  функція має різні знаки.
функція має різні знаки.
Дата добавления: 2018-04-15; просмотров: 1782; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
