ТЕОРЕМА БАНАХА ТА ЇЇ ЗАСТОСУВАННЯ
Існує багато теорем пов’язаних з існуванням розв’язку рівнянь (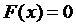 
, диференціальних рівнянь, інтегральних, СЛАР), які можуть бути доведені з єдиної точки зору: шляхом доведення існування нерухомої точки деякого відображення.
Означення. Точка x зветься нерухомою точкою відображення метричного простору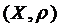 
в себе, якщо справедливою є рівність 
.
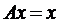Означення. Відображення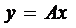 
метричного простору 
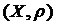в себе зветься стискуючим, або просто стиском, якщо існує таке число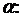 
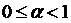, що виконується нерівність: 
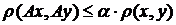. Тобто відстань між образами не перевищує відстань між прообразами.
Теорема. Усяке стискуюче відображення є неперервним.
Доведення. Доведення проведемо на мові послідовностей, тобто за Гейне. Нехай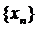 
– довільна послідовність, яка збігається до елемента 
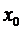. Тобто 
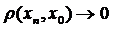, при 
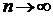. Запишемо умову стиску: 
, 
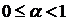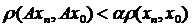. При ,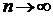 
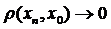, отже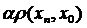 
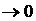, звідки вираз у лівій частині теж прямує до нуля, що означає, що послідовність 
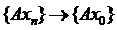. Звідки слідує неперервність відображення.
Терема доведена.
Теорема (Банаха).Усяке стискуюче відображення, яке переводить повний простір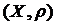 
в себе, має в цьому просторі одну і тільки одну нерухому точку x, або що те саме, що рівняння 
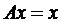має єдиний корінь x.
Доведення. Дано: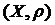 
– повний простір;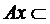 
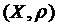– відображення в себе;
, 
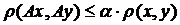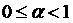– стискуюче відображення.
Треба довести, що існує елемент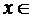 
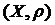, такий що 
.
|
|
|
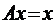Нехай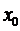 
– довільна точка з простору 
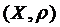. Побудуємо послідовність таким чином:
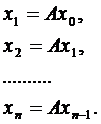
Отримали в просторі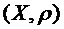 
деяку послідовність 
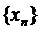. Покажемо, що така послідовність є фундаментальною. Не зменшуючи загальності, будемо вважати, що 
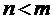. Оцінимо:
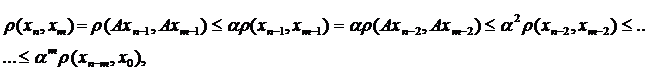
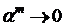, коли 
.
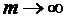Невідомою залишається поведінка другого множника. Оскільки простір метричний, то ми можемо використати нерівність трикутника:
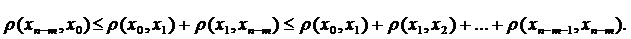Оцінимо кожен доданок починаючи з другого даної нерівності:
,
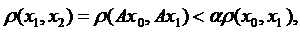
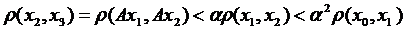Аналогічно будемо мати:
………………………….
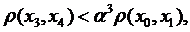
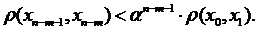
Далі очевидно:
.
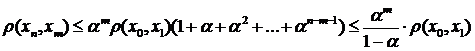Оскільки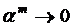 
, коли 
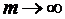, а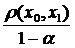 
є якась фіксована стала, то і весь вираз у правій частині при 
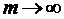теж прямує до нуля. Це означатиме, що наша послідовність є фундаментальною. Оскільки простір у нас повний, то фундаментальна послідовність матиме в цьому просторі границю: 
.
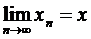Покажемо, що x буде нерухомою точкою відображення, тобто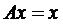 
. Маємо: 
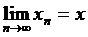, а 
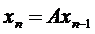. Відображення А є неперервним, отже якщо 
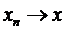при 
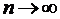, то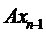 
буде прямувати до 
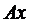, тобто матимемо, що 
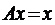при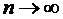 
, що й означає, що x – нерухома точка відображення.
Покажемо, що ця точка єдина.
Нехай існує y, таке що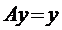 
, тоді матимемо, що 
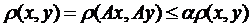. Отже ми отримали, що: 
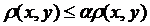, це можливо лише тоді, коли 
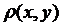=0. Оскільки простір метричний, тоді за першою аксіомою метрики слідує, що 
.
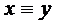Теорему доведено.
|
|
|
Зауваження 1. В процесі доведення теореми Банаха ми не тільки довели існування нерухомої точки, а й вказали спосіб її наближеного відшукання. Цей метод носить назву методу послідовних наближень. Кінцевий результат не залежить від вибору нульового наближення x0. Цей факт з обчислювальної точки зору представляє значний інтерес, бо кожне з наступних наближень ми можемо прийняти за x0, що не дасть накопичуватись похибкам, які будуть залежати від початкового наближення.
Зауваження 2. На практиці обчислення припиняють на якомусь кроці. Тоді виникає питання, як оцінити похибку між точним результатом і наближеним. Скористаємось нерівністю, яку отримали в процесі доведення теореми:
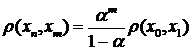, при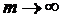 
матимемо: 
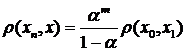. Дана оцінка показує, що послідовні наближення збігаються до точного розв’язку із швидкістю геометричної прогресії.
Дата добавления: 2018-04-15; просмотров: 959; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!