ВІДОБРАЖЕННЯ МЕТРИЧНИХ ПРОСТОРІВ

Границя і неперервність. Критерій неперервності.

Нехай маємо два метричних простори (X,ρ_x), (Y,ρ_y) і множину Е (X,ρ_x).

Означення. Якщо кожному елементу 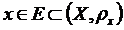 поставлено у відповідність цілком певний елемент у із простору (Y,ρ_y), то кажуть, що задано відображення множини Е в простір (Y,ρ_y) та позначають:  або y=Ax.

Поняття відображення є узагальненням поняття функції. Це може бути числова функція однієї змінної, багатьох змінних, функціонал. У функціональному аналізі відображення, яке елементу довільної природи х ставиться у відповідність елемент  довільної природи у, прийнято ще називати оператором.

Приклади.

1) ;

2)

3)  – функціонал;

   4)

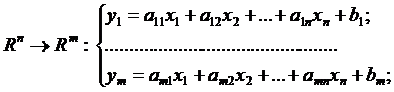
   5)

   6) Розглянемо многочлен Бернштейна:  Це відображення кожній неперервній функції  ставить у відповідність многочлен Бернштейна. Функція  задається на сегменті [0,1]. Особливість многочлена Бернштейна в тому, що він може наблизити як завгодно точно будь-яку неперервну функцію  на [0,1].

За рахунок степеня многочлена n, можна досягти того, що різниця між функцією і многочленом Бернштейна буде як завгодно мала.

Нехай x₀ – гранична точка множини Е, і вона не обов’язково належить множині Е, яка входить у простір (X,ρ_x).

Означення (за Коші). Елемент А, який належить простору (Y,ρ_y) називається границею відображення  при 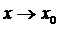, якщо для таке що, як тільки то .

Означення (за Гейне). Елемент А називається границею відображення  при 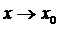, якщо із збіжності будь-якої послідовності  випливає збіжність відповідної послідовності значень відображення  до А. (Тут збіжність розуміється як збіжність за відстанню).

Нехай тепер відображення визначене в точці x₀.

Означення. Відображення  називається неперервним у точці x₀, якщо для , що як тільки то .

Означення. Відображення  називається неперервним в точці x₀, якщо із збіжності будь-якої послідовності 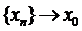 випливає збіжність .

Якщо відображення взаємооднозначне, то для нього існує обернене відображення.

Означення. Взаємнооднозначне і неперервне відображення називається гомеоморфізмом.

Означення. Гомеоморфне відображення називається ізометрією, або ізоморфізмом, якщо воно зберігає відстань між образами.

Теорема (критерій неперервності). Щоб відображення 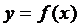 було неперервним необхідно і достатньо, щоб прообраз  був відкритим для всякої відкритої множини G, яка входить в Y.

Доведення. Необхідність. Дано, що відображення  – неперервне і множина G  – відкрита. Треба довести, що  – відкрита, тобто всі її точки внутрішні. Нехай , . Покажемо, що точка x₀ належить множині  разом з своїм околом. Оскільки y₀ є внутрішньою точкою множини G, то існує , що куля . В силу неперервності відображення по заданому  ми знайдемо таке , що як тільки  попадає в кулю , то y попадає в кулю . Ясно, що куля  належить множині праобразів , це означає, що  разом із деяким своїм околом, а це означає, що  є відкритою множиною (в силу довільності вибраної точки x₀).

Достатність. Дано  – відкрита куля, для будь-якої відкритої множини . Доведемо неперервність відображення. Нехай  – довільна точка множини  і нехай . Для  розглянемо кулю . За умовою образ даної кулі: – є відкрита множина, тобто всі її точки внутрішні, а отже і точка , це означає, що знайдеться таке , що куля  попаде в кулю , а це і означає неперервність даного відображення у точці x₀ за Коші.

Теорему доведено.

 

---

Дата добавления: 2018-04-15; просмотров: 319; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!