Приклади метричних просторів.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
РІВНЕНСЬКИЙ ДЕРЖАВНИЙ ГУМАНІТАРНИЙ
УНІВЕРСИТЕТ
Кафедра вищої математики
І.М. Присяжнюк, В.К. Столярчук,
О.В. Романів
ФУНКЦІОНАЛЬНИЙ АНАЛІЗ
Курс лекцій, індивідуальних завдань і методичних вказівок до їх виконання для студентів стаціонарної форми навчання спеціальностей "прикладна математика" та "інформатика"
Рівне - 2008
Посібник містить курс лекцій, приклади розв'язання типових задач, тексти індивідуальних завдань з курсу "Функціональний аналіз", питання до екзамену.
Рецензент: кандидат фізико-математичних наук, професор кафедри вищої математики Петрівський Б.П.
Рекомендовано до друку на засіданні кафедри вищої математики, протокол №__від_____2008р.
© І.М. Присяжнюк, В.К. Столярчук, О.В. Романів, 2008
ЗМІСТ
1. Вступ. Короткі історичні відомості 4
2. Метричні простори 6
3. Послідовності в метричних просторах. Збіжність 13
4. Відображення метричних просторів 24
Повнота метричних просторів 30
Теорема Банаха та її застосування 37
|
|
|
7. Компакти 53
Лема Гейне-Бореля 60
Лінійні, нормовані та евклідові простори 68
Лінійні оператори і лінійні функціонали 77
Лінійні додатні оператори 83
Контрольна робота 87
Програмні питання до екзамену 89
Рекомендована література 91
ВСТУП. КОРОТКІ ІСТОРИЧНІ ВІДОМОСТІ
Функціональний аналіз – вiдносно молода галузь сучасної математики, яка виникла на рубежі ХІХ – ХХ ст. на стику лінійної алгебри, геометрії та математичного аналізу.
 Взагалі, початком самостійного існування функціональого аналізу можна вважати систематизовану побудову теорії операторів (Гільберт), і розвиток загальної теорії лінійних нормованих просторів (1918–1923р., український математик Стефан Стефанович Банах).
Взагалі, початком самостійного існування функціональого аналізу можна вважати систематизовану побудову теорії операторів (Гільберт), і розвиток загальної теорії лінійних нормованих просторів (1918–1923р., український математик Стефан Стефанович Банах).
|
|
|
Історична довідка
Банах Степан, син горянки Катерини Банах та Гречека Степана, мешканця Кракiвського староства (30 березня 1892 — 31 серпня 1945).
 Народився у Краковi, поляк. Після народження батько віддав його на виховання до сім'ї краківської прачки. Пiсля закічення Кракiвської гімназії у 1910 р. вступив на факультет машинобудування Львівської політехнічної школи. У 1911 р. перевівся на факультет інженерії за спеціальністю «Сухопутна інженерія», де закінчив четвертий останній (1913—1914) навчальний рік. З 1920 до 1922 р. працював асистентом на кафедрі математики Львівської політехніки у професора А.Ломніцького. Опублiкував ряд наукових праць. У 1920 р. здобув учений ступінь доктора філософії, а в 1924 р. був затверджений у вченому званні надзвичайного професора кафедри математики Львівського університету i обраний членом-кореспондентом ПАН. У 1927 р. став звичайним професором. Один із творців сучасного функціонального аналізу, разом з Г. Штайнгаузом в 1929 р. організував видання відомого журналу «Studia mathematica».
Народився у Краковi, поляк. Після народження батько віддав його на виховання до сім'ї краківської прачки. Пiсля закічення Кракiвської гімназії у 1910 р. вступив на факультет машинобудування Львівської політехнічної школи. У 1911 р. перевівся на факультет інженерії за спеціальністю «Сухопутна інженерія», де закінчив четвертий останній (1913—1914) навчальний рік. З 1920 до 1922 р. працював асистентом на кафедрі математики Львівської політехніки у професора А.Ломніцького. Опублiкував ряд наукових праць. У 1920 р. здобув учений ступінь доктора філософії, а в 1924 р. був затверджений у вченому званні надзвичайного професора кафедри математики Львівського університету i обраний членом-кореспондентом ПАН. У 1927 р. став звичайним професором. Один із творців сучасного функціонального аналізу, разом з Г. Штайнгаузом в 1929 р. організував видання відомого журналу «Studia mathematica».
Вивчені ним лінійні простори, що одержали назву "простори Банаха" мають велике значення для сучасної математики. Разом зі своіми учнями — С. Мазуром, В. Орличом, В. П. Шаудером — став одним із фундаторів (згодом — із світовим визнанням) Львівської математичної школи, в якій розроблено значну частину функціонального аналізу. Багато його результатів стали класичними i входять до підручників та монографій з функціонального аналізу. Деякі роботи стосуються теорії звичайних диференціальних рівнянь (Банахове середнє), теорії функцій комплексної змінної та ін. Основні твори (зокрема «Теорiя лінійних операторів», «Диференційне та інтегральне числення») опубліковано польською, французькою та українською мовами. 3 1939 р. — Голова Польського математичного товариства, член-кореспондент АН УРСР, лауреат великої премії ПАН. Працював деканом фізико-математичного факультету Львівського університету i одночасно перебував на керівній роботі в інституті АН УРСР (Львівська філія). Пiд час німецької окупації спочатку переховувався, а потім — аби якось прожити — вступив до протитифозного інституту Вейгля, де прославленого математика використовували як об'ект ризикованих i принизливих для людської гідності медичних експериментів. У 1944 р. факультет ЛДУ: за сумісництвом завідував кафедрою теоретичної механіки ЛПI. Його відкриття стали золотим фондом математики XX ст. Польське математичне товариство заснувало премію ім. С. Банаха. Похований на Личакiвському цвинтарі.
|
|
|
|
|
|
Одним з основних понять функціонального аналізу є поняття метричного простору.
Метричний простір – множина об’єктів довільної природи, для яких введено поняття відстані між елементами (числами, n-дійсними числами, n-вимірними векторами, функціями, наборами функцій і т.д.).
Другим важливим поняттям функціонального аналізу є поняття оператора, яке є узагальненням поняття функції. Якщо числу у відповідність ставиться число, то це числова функція однієї змінної (  ); n-вимірному вектору ставиться у відповідність число, то це числова функція багатьох змінних (
); n-вимірному вектору ставиться у відповідність число, то це числова функція багатьох змінних (  ); для функції у відповідність ставиться число, то це функціонал (
); для функції у відповідність ставиться число, то це функціонал (  ).
).
Якщо елементу довільної природи ставиться у відповідність елемент довільної (або відповідної) природи, то це оператор відображення.
Твердження функціонального аналізу носять загальний характер. В залежності від того, яким буде метричний простір і яким буде оператор, ми одержимо твердження з алгебри, геометрії чи математичного аналізу. Здобутки функціонального аналізу мають широке застосування в лінійній алгебрі, квантовій фізиці, хімії та в теорії диференціальних і інтегральних рівнянь, обчислювальній математиці, дослідженні збіжних процесів, оцінок похибок.
МЕТРИЧНІ ПРОСТОРИ
Поняття границі – основне поняття математичного аналізу, за допомогою якого вводиться поняття похідної, інтеграла та ін. Саме поняття границі використовує поняття відстані між числами. Дійсно, той факт, що числова послідовність 
 означає, що
означає, що  . Щоб ввести поняття границі для більш складніших об′єктів ніж число, потрібно означити поняття відстані між абстрактними об′єктами, що приводить до поняття метричного простору.
. Щоб ввести поняття границі для більш складніших об′єктів ніж число, потрібно означити поняття відстані між абстрактними об′єктами, що приводить до поняття метричного простору.
Означення.Множина об′єктів довільної природи {х,у,z,…} називається метричним простором, якщо на цій множині визначено поняття відстані r(х,у), яка будь-яким двом елементам х та у ставить у відповідність число r(х,у), яке задовольняє трьом аксіомам:
1. r(х,у)³0 , r(х,у)=0 Û xºy – рефлексивність відстані;
2. r(х,у)= r(у,x) – симетричність відстані;
3. r(х,у)£ r(х,z)+ r(z,у) – нерівність трикутника.
Метричний простір з множиною елементів Х та заданою відстанню r, позначають (Х,r).
Приклади метричних просторів.
1. Простір R1, Х – елементами є дійсні числа, відстань визначається так:
r(х,y)=  .
.
Перевіримо, чи даний простір буде метричним. Для цього повинно виконуватись три аксіоми метрики.
а) r(х,у)³0 – в силу властивостей модуля дійсного числа. Якщо r(х,у)=0 
 . Якщо
. Якщо  , то r(х,у)= r(y,у)=
, то r(х,у)= r(y,у)=  .
.
Першу аксіому довели. Далі маємо:
б) r(х,у) =  =
=  .
.
в) r(х,у) = 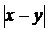 =
= 

2. Простір ізольованих точок. {х,у,z,…} – елементи довільної природи,

Виконання аксіом відстані перевірити самостійно.
3. Простір Rn , x=(x1,x2,…,xn), y=(y1,y2,…,yn),  .
.
Перевіримо три аксіоми метрики:
а) r(х,у)³0 – випливає із властивостей квадрата числа, суми, та кореня квадратного.
Якщо х=у, то r(х,у)=r(х,х)=  =0. Нехай r(х,у)=0, тоді
=0. Нехай r(х,у)=0, тоді  =0. Звідси слідує, що
=0. Звідси слідує, що  (
(  ), а це означає, що х=у. Перша аксіома доведена.
), а це означає, що х=у. Перша аксіома доведена.
б) ρ(х,у)= 
в) Доведемо нерівність трикутника, використовуючи для цього нерівність Коші-Буняковського:
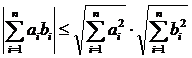 .
.
Розглянемо квадрат відстані ρ(х,у):
(ρ(х,у))2=  =
=  =
= 

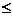 (до другого доданка застосуємо нерівність Коші-Буняковського)
(до другого доданка застосуємо нерівність Коші-Буняковського) 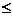
 +
+ 
 = =(ρ(x,z)+ρ(z,y))2.
= =(ρ(x,z)+ρ(z,y))2.
Отже, (ρ(х,у))2 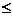 (ρ(x,z)+ρ(z,y))2. Оскільки права і ліва частини нерівності є невід′ємними, то квадрат можемо прибрати, тоді отримаємо нерівність трикутника.
(ρ(x,z)+ρ(z,y))2. Оскільки права і ліва частини нерівності є невід′ємними, то квадрат можемо прибрати, тоді отримаємо нерівність трикутника.
4.Простір  , x=(x1,x2,…,xn), y=(y1,y2,…,yn), ρ(x,y) =
, x=(x1,x2,…,xn), y=(y1,y2,…,yn), ρ(x,y) =  .
.
Доведемо третю аксіому:

Дана нерівність виконується при будь-якому і, а отже і для максимуму. Матимемо:

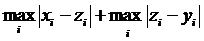 .
.
5.Простір  із заданою відстанню ρ(х,у) =
із заданою відстанню ρ(х,у) =  Аксіоми доводяться аналогічно до попередніх випадків. (x=(x1,x2,…,xn) – елемент простору).
Аксіоми доводяться аналогічно до попередніх випадків. (x=(x1,x2,…,xn) – елемент простору).
6.Простір  , елементами в якому є нескінчені послідовності виду x=(x1,x2,…,xn,…) і виконується умова
, елементами в якому є нескінчені послідовності виду x=(x1,x2,…,xn,…) і виконується умова  . Відстань задається наступним чином: ρ(х,у) =
. Відстань задається наступним чином: ρ(х,у) =  .
.
Перевіримо коректність введеної метрики, а саме, переконаємося, що ряд, який фігурує під знаком радикала, збіжний. Маємо, що:  і те, що ряди із загальними членами
і те, що ряди із загальними членами 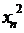 та
та  – збіжні. Тоді і сума цих рядів збіжна. Звідси випливає, що і ряд із загальним членом у правій частині останньої нерівності (
– збіжні. Тоді і сума цих рядів збіжна. Звідси випливає, що і ряд із загальним членом у правій частині останньої нерівності ( 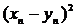 ) також збігається. Аксіоми відстані перевіряються так само, як це робилося для простору Rn.
) також збігається. Аксіоми відстані перевіряються так само, як це робилося для простору Rn.
7.Простір С[a,b] – простір неперервних функцій на відрізку  елементом, якого є x=x(t). Відстань вводиться наступним чином:
елементом, якого є x=x(t). Відстань вводиться наступним чином:
 .
.
Доведемо третю аксіому. Для будь-якого t є  маємо:
маємо: 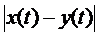 =
=  +
+ 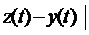



 . Знову ж, якщо така нерівність виконується для будь-якого t є
. Знову ж, якщо така нерівність виконується для будь-якого t є  , то вона буде виконуватись і для
, то вона буде виконуватись і для  , тобто:
, тобто:  , тим самим довели нерівність трикутника.
, тим самим довели нерівність трикутника.
8. Простір CL – простір неперервних на відрізку  функцій із відстанню
функцій із відстанню  .
.
Доведемо першу аксіому.  в силу властивостей модуля числа та інтеграла. Нехай x(t)=y(t), тоді
в силу властивостей модуля числа та інтеграла. Нехай x(t)=y(t), тоді  =
=  =
=  =0. Якщо
=0. Якщо 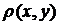 =0, то міркуємо так: нехай існує точка t0 в якій х(t0)
=0, то міркуємо так: нехай існує точка t0 в якій х(t0)  y(t0) і х(t0)>y(t0), тоді в силу неперервності функцій х(t) і y(t), х(t)>y(t) в деякому околі t0. Тоді матимемо, що
y(t0) і х(t0)>y(t0), тоді в силу неперервності функцій х(t) і y(t), х(t)>y(t) в деякому околі t0. Тоді матимемо, що  >0. Прийшли до суперечності. Звідси слідує, що x(t)має дорівнювати y(t). Другаі третя аксіоми доводяться аналогічно до попередніх випадків.
>0. Прийшли до суперечності. Звідси слідує, що x(t)має дорівнювати y(t). Другаі третя аксіоми доводяться аналогічно до попередніх випадків.
9.Простір  – простір неперервних функцій на
– простір неперервних функцій на  , метрика якого вводиться так:
, метрика якого вводиться так:
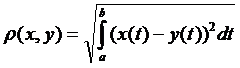 .
.
Доведемо нерівність трикутника. Для цього скористаємося інтегральною нерівністю Коші-Буняковського:
 .
.
Маємо: 

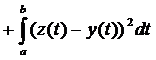 =
=
=  .
.
Добуваючи квадратний корінь з невід’ємних чисел, отримаємо нерівність трикутника.
10. Простір C0 – елементами якого є нескінчені послідовності, що збігають до нуля: x=(x1,x2,…,xn,…),  ,
,  . Таке означення відстані є коректним, бо
. Таке означення відстані є коректним, бо  . А оскільки послідовності {xi} i {yi} збігаються до нуля, то вони обмежені довільним числом. Тоді
. А оскільки послідовності {xi} i {yi} збігаються до нуля, то вони обмежені довільним числом. Тоді  , як величина обмежена, має супремум. Виконання аксіом відстані очевидне.
, як величина обмежена, має супремум. Виконання аксіом відстані очевидне.
11.Простір Cm – х – довільна обмежена послідовність.  ,
, 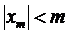 . Пропонуємо читачеві самостійно перевірити виконання аксіом метрики та коректність такого означення відстані
. Пропонуємо читачеві самостійно перевірити виконання аксіом метрики та коректність такого означення відстані
Контрольні запитання.
1. Дати означення метричного простору.
2. Дати означення метричних просторів ізольованих точок, 
3. Записати нерівність Коші-Буняковського для інтегралів і вказати схему її доведення.
4. Чи можна в просторі С[a,b] відстань означити за формулою 
5. Які метричні простори вивчаються в курсі математики середньої школи, курсі лінійної алгебри, математичного аналізу, теорії рядів Фур’є.
Вправи.
1. Перевірити аксіоми метрики для простору ізольованих точок.
2. Дано  =sin
=sin  |x – y|, x,y
|x – y|, x,y  , чи буде
, чи буде  метрикою.
метрикою.
3. Дано простір С[a,b]. Чи можна в ньому ввести відстань за формулою  =
=  |x(t) – y(t)|.
|x(t) – y(t)|.
4. Дано x  ,
,  =arctg|x – y|. Чи буде
=arctg|x – y|. Чи буде  метрикою.
метрикою.
Розв’язання.
1. Дано  =
=  .
.
Виконання першої і другої аксіом метрики очевидне. Перевіримо чи виконується аксіома трикутника 
 .
.
Припустиму протилежне, що дана нерівність не виконується. Це можливо тоді, коли в лівій частині буде одиниця (x  y), а в правій частині – нуль, тобто x=z, z=y. Звідси випливає, що x=y. А це суперечить припущенню, що x
y), а в правій частині – нуль, тобто x=z, z=y. Звідси випливає, що x=y. А це суперечить припущенню, що x  y.
y.
2. Ні, не буде, тому що не виконується перша аксіома метрики. А саме: з того, що відстань рівна нулю, ще не випливає що x=y. (З рівності sin  |x–y|=0
|x–y|=0  sin|x–y|=0
sin|x–y|=0  (x–y)=k
(x–y)=k  , k
, k 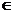 Z,
Z,  , k
, k 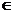 Z, x=
Z, x=  k
k  ).
).
3. Ні, тому, що не виконуватиметься перша аксіома метрики. Справді, взявши дві неперервні функції x(t) і y(t), які перетинаються, наприклад, в одній точці ми матимемо, що  =0. Однак ці функції тотожно не співпадають.
=0. Однак ці функції тотожно не співпадають.
4. Виконання першої і другої аксіом відстані очевидне. Доведемо нерівність трикутника:
 =arctg |x–y|= arctg |x–z+z–y|
=arctg |x–y|= arctg |x–z+z–y| 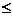 arctg (|x–z|+(z–y)|
arctg (|x–z|+(z–y)| 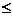
 arctg |x–z|+ arctg |z–y|=
arctg |x–z|+ arctg |z–y|=  +
+ 
(передостанню нерівність пропонуємо довести самостійно).
Задачі.
1. Перевірити аксіоми метрики для простору  .
.
2.  метрика. Довести, що
метрика. Довести, що  також метрика.
також метрика.
3. Дано, що  – метрика. Довести, що
– метрика. Довести, що  також метрика.
також метрика.
4. Дано:  . Перевірити аксіоми метрики.
. Перевірити аксіоми метрики.
5. Дано множину диференційованих функцій x(t),  Перевірити аксіоми метрики.
Перевірити аксіоми метрики.
6. Дано 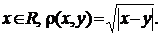 Перевірити виконання аксіом метрики.
Перевірити виконання аксіом метрики.
7. Дано 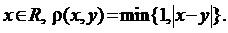 Перевірити виконання аксіом метрики.
Перевірити виконання аксіом метрики.
8. Дано 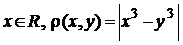 . Чи буде
. Чи буде  метрикою.
метрикою.
9. Дано 
 . Чи буде
. Чи буде  метрикою.
метрикою.
10. Дано  . Чи буде
. Чи буде  метрикою.
метрикою.
Дата добавления: 2018-04-15; просмотров: 1330; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
