Повнота деяких важливих метричних просторів.

Теорема 1. Простір Rⁿ – повний.

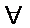
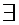Доведення. Розглянемо довільну фундаментальну послідовність у цьому просторі . Отже, N, що як тільки m,k > N, то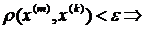

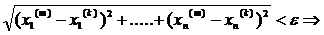
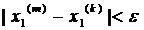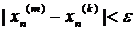,…, , а це є умови фундаментальності послідовностей відповідних координат в просторі R¹, але простір R¹ – повний, тому будуть існувати границі: ,…, .

Складемо елемент простору Rⁿ , який і буде границею нашої фундаментальної послідовності (оскільки в цьому просторі по координатна збіжність рівносильна збіжності за відстанню).

Теорему доведено.

Теорема 2. Простір С_[_a_,_b_] – повний.

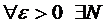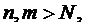
Доведення. Нехай { } – довільна фундаментальна послідовність. Для , 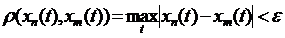. Обґрунтуємо існування границі даної послідовності. Зафіксуємо 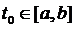, одержимо числову послідовність , яка буде фундаментальною, і тому в цьому просторі вона матиме границю x(t₀). Оскільки t₀ми вибрали довільно, то буде існувати границя при . Позначимо її через x(t).

Перейшовши в нерівності 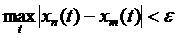до границі, коли , дістанемо . Остання нерівність означає, що x_m(t)прямує до граничної функції рівномірно. Тоді за відомою теоремою з математичного аналізу неперервна.

Теорему доведено.

Теорема 3. Простір – повний.

Доведення. Розглянемо в цьому просторі довільну фундаментальну послідовність 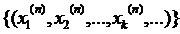. Причому ряд 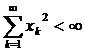– збіжний. Запишемо умову фундаментальності: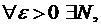

....................................

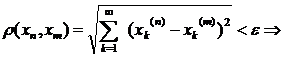
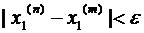Останні нерівності означають, що числові послідовності координат фундаментальні. Але простір R¹ – повний, тому існують границі:

..........................

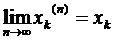Складемо такий вектор 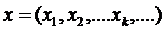. Він і буде границею вихідної фундаментальної послідовності.Для цього достатньо показати, що

1) послідовність 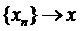за метрикою даного простору;

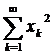2) , тобто ряд – збіжний.

Доведемо коротко перший факт.

Оскільки послідовність фундаментальна, то справедливою буде нерівність: 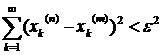, для 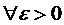і таког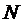о , що 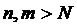. Тоді для 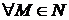будемо мати: 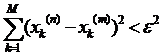. Здійснимо граничний перехід при , і будемо мати: 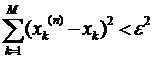. Оскільки М – довільне, матимемо: , а це і означає, що вибрана послідовність прямує до граничного вектора: .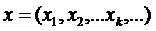

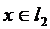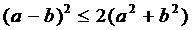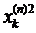Доведемо другий факт, а саме що , тобто ряд – збіжний. Використаємо нерівність . Поклавши , і, підставивши їх в нерівність, отримаємо: . Ряди, членами яких є та 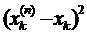є збіжними, звідси слідує, що ряд членами, якого є 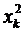також буде збіжним, а це означає, що граничний елемент 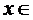l₂. Отже, l₂– повний.

Теорему доведено.

Означення. Метричний простір R^* називається поповненням простору R, якщо виконується три умови:

1. Простір 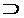R^* R,

2. R всюди щільний в просторі R^*,

3. R^* – повний.

Теорема. Усякий неповний метричний простір R можна поповнити, і причому єдиним чином.

Контрольні запитання.

1. Дати означення повного метричного простору.

2. Сформулювати теорему про вкладені кулі.

3. Довести, що замкнений підпростір повного простору – повний.

4. Довести повноту просторів: Rⁿ, l₂, С_[_a_,_b_] .

5. Сформулювати теорему про поповнення простору.

Вправи.

1. Дано множину натуральних чисел 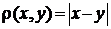. Довести, що даний простір повний.

2. Дано множину натуральних чисел N, 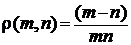. Довести, що даний простір не повний.

3. Дано множину ірраціональних чисел 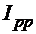, 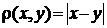. Дослідити цей простір на повноту.

4. Дослідити на повноту простір .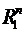

Розв’язання.

1. Розглянемо у даному просторі довільну фундаментальну послідовність натуральних чисел. Вона обов’язково матиме таку структуру: скінченна кількість перших її членів буде довільними натуральними числами, а починаючи з деякого номера одне з натуральних чисел буде повторюватись, інакше послідовність не буде фундаментальною. Тоді ясно, що це натуральне число яке повторюється і буде границею послідовності.

2. Даний простір не є повним. Щоб це довести, достатньо вказати хоч одну фундаментальну послідовність, яка в цьому просторі не матиме границі. Такою послідовністю буде послідовність натуральних чисел 1,2,3…,n,… Справді, ця послідовність за даною метрикою буде фундаментальною, бо вираз 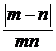можна зробити як завгодно малим при достатньо великих m і n. Однак ця послідовність не матиме границі. Бо якби така границя існувала і дорівнювала б натуральному числу а, то ми мали б, що 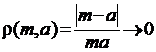. Насправді ж, наприклад при 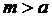маємо при .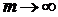

3. Даний простір не є повним, тому що, наприклад, фундаментальна послідовність 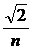ірраціональних чисел у цьому просторі не має границі. (Послідовність прямує до нуля, який не є ірраціональним числом).

4. Розглянемо в цьому просторі довільну фундаментальну послідовність 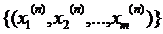. Це означає, що для будь якогo >0 існує номер N такий, що при , виконується нерівність 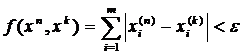i=1,2,...,m. Це означає, що числові послідовності координат фундаментальні. Але простір R¹– повний, так що ці числові послідовності матимуть границі: 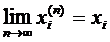, i=1,2,...,m. Складемо вектор . Він і буде границею вихідної послідовності, бо збіжність за відстанню у просторі R рівносильна покоординатній збіжності.

Задачі.

Дата добавления: 2018-04-15; просмотров: 406; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!