Властивості неперервних відображень компактів.

Теорема 1. Неперервний образ компакту є компакт.

Доведення. Дано, що E – компакт, f(x) – неперервне відображення. Розглянемо довільну послідовність y₁,...,y_n, яка належить f(E) і покажемо, що з неї можна виділити збіжну підпослідовність, границя якої належить множині образів. Розглянемо відповідну послідовність прообразів x₁,...,x_n. Вона належить 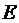, а отже з неї можна виділити збіжну підпослідовність 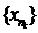, таку що 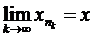, 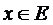. Тоді в силу неперервності відображення 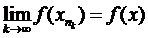, , 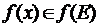бо x належить множині прообразів.

Теорема 2. Нехай маємо неперервне і взаємнооднозначне відображення 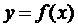компакту E на множину Y. Тоді обернене відображення 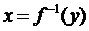теж неперервне.

Доведення. Припустимо протилежне, що обернене відображення не є неперервним у довільній точці y. Тоді за означенням неперервності за Гейне буде існувати послідовність 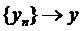, однак, 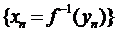не прямує до 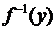. Це означає, що можливі два випадки:

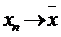
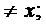
2. 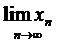– не існує.

1. В силу неперервності прямого відображення 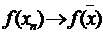, а за умовою 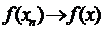, тоді маємо, що послідовність має дві границі, що неможливо.

2. 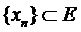, то з цієї послідовності можна виділити збіжну підпослідовність границя, якої належить Е, бо Е – компакт. Отже, буде існувати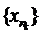 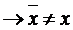. Тоді в силу неперервності 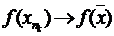, а це суперечить тому, що 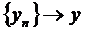. Оскільки 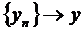, то будь-яка підпослідовність 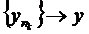. Прийшли до суперечності.

Теорему доведено.

Рівномірно неперервні відображення. Теорема Кантора.

Означення. Відображення f(x) називається рівномірно неперервним на множині 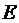, якщо для , .

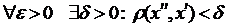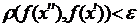Теорема (Кантора). Якщо відображення 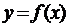– неперервне на компакті Е, то воно рівномірно неперервне на ньому.

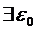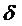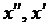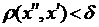Доведення. Нехай відображення не є рівномірно неперервним. Тоді , що яке б ми не брали, знайдеться хоча б два елементи , що як тільки , то 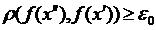. В силу довільності 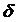, виберемо його так: 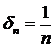, 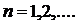. Для кожного 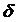існуватиме пара точок 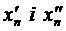, що як тільки 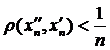, то 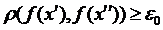(*). Отримали дві послідовності 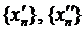, які належать 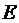. Тоді з послідовності 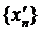можна виділити збіжну підпослідовність з границею x₀. Щоб не вводити нових індексів, будемо вважати, що 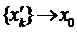. Покажемо, що .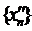

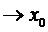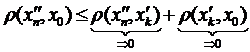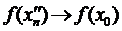Дійсно: . Тоді в силу неперервності відображення і , а це суперечить (*), бо:

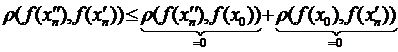Теорему доведено.

Числові функції на компакті.

Відображення 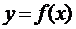, , 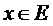яке елементу довільної природи x ставить у відповідність число називається функціоналом.

Перша теорема Вейєрштрасса. Якщо числова функція 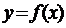неперервна на компакті Е, то вона обмежена на ньому.

Доведення. Неперервний образ компакту є компакт, а компакт є множина обмежена, що і доводить теорему.

Друга теорема Вейєрштрасса. Якщо числова функція 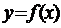неперервна на компакті 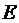, то вона досягає на ньому свого найбільшого і найменшого значення.

Доведення. За попередньою теоремою 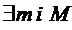, що 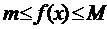. Якщо функція обмежена знизу і зверху, то вона має свою точну верхню і нижню грані. 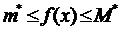. Доведемо для означеності, що f(x) досягає свого 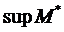, де 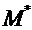– гранична точка f(E), бо у будь-якому її околі є нескінченна кількість точок з f(E). А оскільки f(E) замкнена, то .

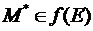Контрольні запитання.

1. Навести приклад простору в якому не виконується теорема Больцано-Вейєрштрасса.

2. Дати означення компакту.

3. Сформулювати основні властивості компактів.

4. Охарактеризувати компакти в просторі .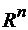

5. Вказати схему доведення теореми про компактність образу при неперервному відображенні.

6. Сформулювати теорему про неперервність оберненого відображення.

7. Сформулювати першу і другу теореми Вейєрштрасса та теорему Кантора про властивості числових функцій на компакті.

Вправи.

1. Дослідити на копактність простір ізольованих точок.

2. Довести, що сегмент є компактним.

3. Довести першу теорему Вейєрштрасса про обмеженість неперервної числової функції на компакті використовуючи властивості компактності.

4. Дослідити на копактність інтервал (0,1).

Розв’язання.

1. Розглянемо довільну послідовність із простору ізольованих точок. Оскільки послідовність нескінченна, то одна або кілька точок будуть повторюватись. Тоді ясно, як з такої послідовності можна виділити збіжну підпослідовність.

2. Візьмемо довільну числову підпослідовність, яка належить сегменту . За теоремою Больцано-Вейєрштрасса з неї можна виділити збіжну підпослідовність, границя якої, в силу замкненості сегменту, належатиме .

3. Оскільки неперервний образ компакту є компакт, а компакт є множина обмежена, то звідси і випливає, що множина значень неперервної функції f(x), x 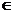буде обмеженою, що і доводить першу теорему Вейєрштрасса.

4. Інтервал (0,1) не є компакт, бо послідовність (значить і будь-яка її підпослідовність) прямує до нуля, коли 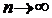, а нуль не належить проміжку (0,1).

Задачі.

1. Дослідити на копактність множину раціональних і ірраціональних точок сегменту [0,1].

2. Довести що замкнений одиничний квадрат з простору 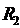є компакт.

3. Довести, що всякий компакт є множина замкнена і обмежена.

4. Довести, що перетин двох компактів є компакт.

5. Довести, що об’єднання двох компактів є компакт.

6. Довести першу і другу теореми Вейєрштрасса про властивості числових функцій на компакті, використовуючи той факт, що компакт є множина замкнена і обмежена.

ЛЕМА ГЕЙНЕ-БОРЕЛЯ

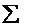Розглянемо разом з проміжком деяку систему відкритих відрізків 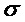, яка може бути як скінченною так і нескінченною. Домовимось, що система 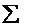покриває проміжок , якщо для кожної точки x 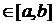найдеться в 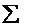проміжок 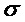, який містить її.

Лема Бореля. Якщо замкнений проміжок покривається нескінченною системою 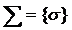відкритих відрізків, то із неї завжди можна виділити скінчену підсистему 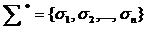,яка також покриє проміжок .

Доведення 1 (Метод Больцано).

Доведення проведемо методом від супротивного. Припустимо проміжок не може бути покритий скінченним числом відрізків 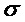із 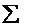. Розділимо проміжок навпіл. Тоді хоча б одна з його половин також не може бути покрита скінченим числом 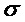. Дійсно, якщо одна із них могла бути покрита відрізками 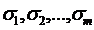(із 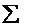), а друга – відрізками 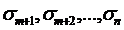(із 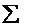), то із всіх цих відрізків склалася б скінченна система 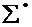, яка б покрила весь проміжок . А це суперечить припущенню. Позначимо через 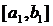ту половину відрізка, яка не покривається скінченним числом 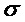(якщо обидві такі, то будь-яку з них). Цей проміжок знову розділимо навпіл і позначимо через 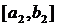ту із його половин, яку не можна покрити скінченим числом 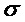, і т. д.

Продовжуючи цей процес, ми одержимо нескінчену послідовність вкладених відрізків 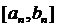( 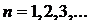), кожен із яких складає половину від попереднього. Всі ці проміжки вибираються так, що жоден з них не покривається скінченним числом відрізків 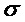. Згідно з лемою про вкладені відрізки, існує спільна їм всім точка c, до якої прямують кінці .

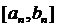Ця точка c, як і будь-яка точка проміжку , лежить в одному із відрізків 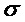, який ми позначимо 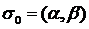, так що 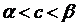. Проте послідовносі {a_n} і {b_n} прямують до c, і починаючи з деякого номера будуть самі лежати між 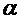і 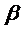, таким чином, що визначений ними проміжок 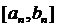виявиться покритим лиш одним відрізком 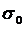, всупереч самому вибору цих проміжків 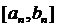. Отримана суперечність і доводить лему.

Доведення 2 (Лебега)

Розглянемо точки 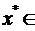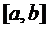, які володіють тими властивостями, що відрізок 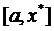покривається скінченим числом відрізків 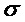. Такі точки 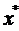, загалом, знайдуться: так як, наприклад, точка a лежить в одному із 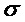, то і всі близькі до неї точки, які знаходяться в даному відрізку 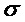, відповідно виявляються точками .

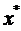Нашою задачею є встановити, що точка b належить до числа точок 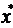. Так як всі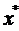 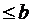, то: 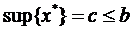. Як і всі точки з проміжку 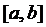, c належить деякому 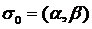, 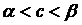. Проте, по властивостям точної верхньої грані, знайдеться 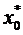, таке що 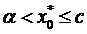. Проміжок 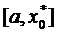покривається скінченим числом відрізків 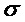(за означенням точок 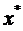), якщо до цих проміжків приєднати ще один відрізок 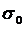, то й покриється весь проміжок 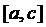, так що c є одною із точок .

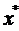Разом з цим, ясно, що c не може бути менше b, бо інакше між c і 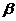знайшлася б ще точка 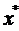, всупереч знаходження числа c, як верхньої межі всіх 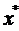. Таким чином, необхідно щоб b=c, значить b є одна із 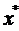, тобто 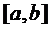покривається скінченим числом відрізків .

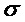Зауважимо, що лема справедлива тоді, коли 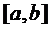– замкнений, а 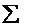– відкриті. Наприклад, система відкритих відрізків: 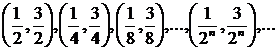покриває проміжок 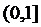, проте з них не можна виділити скінченну підсистему з вище вказаними властивостями. Аналогічно, система замкнених відрізків: 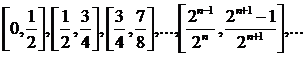та 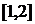, покриває проміжок 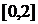, але й тут виділення скінченної підсистеми неможливе.

Дата добавления: 2018-04-15; просмотров: 799; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 5 6 7 8 91011 12 13 14 Следующая ⇒

Мы поможем в написании ваших работ!