Найпростіші застосування теореми Банаха.
Нехай є рівняння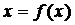 
, де 
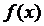– неперервна функція однієї змінної, визначена на 
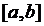і її значення не виходять за межі сегмента 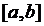(матимемо відображення в себе). Крім того 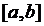є повним простором, як замкнений підпростір повного простору. Нехай виконується умова стиску, тобто: 
, 
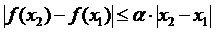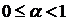. Отже існуватиме єдиний корінь рівняння 
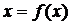, який можемо знайти методом послідовних наближень. Зауважимо, що умова стиску, яку важко перевірити на практиці, буде виконуватися, якщо 
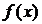має похідну, таку що: 
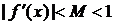. Дійсно, використавши теорему Лагранжа матимемо: 
, 
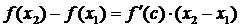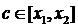. Тоді взявши по модулю ліву та праву частини, отримаємо: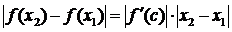 
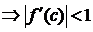. Розглянемо складніший випадок рівняння: 
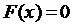. Вихідне рівняння еквівалентне такому рівнянню: 
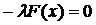. Додамо до обох частин по x: x–λF(x)=x, отримали рівняння 
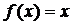із попереднього випадку. Вимагатимемо, щоб виконувався стиск, було відображення в себе, і щоб простір був повний (простір R1 – повний). Вимагатимемо щоб: 
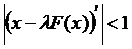, тобто 
, 
, 
.
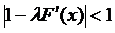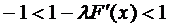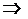
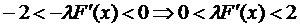
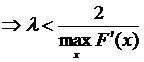Розглянемо систему n лінійних рівнянь з n невідомими:
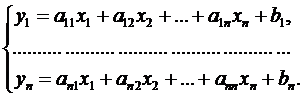
Поставимо задачу розв’язати систему рівнянь в якої замість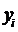 
стоятимуть 
, 
.
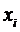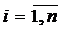По-перше, Rn – простір повний. По-друге, маємо відображення в себе (Rn → Rn). По-третє, вияснимо виконання умови стиску, яка залежатиме від метрики простору Rn. Нехай маємо простір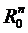 
, тоді: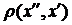 
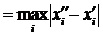, відповідно матимемо: 
.
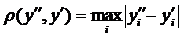Маємо:
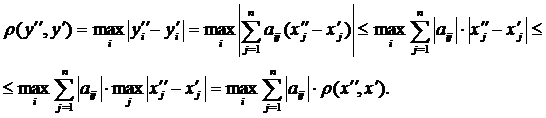
Отже умова стиску буде такою: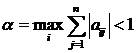 
. Аналогічно доводяться умови стиску для просторів 
: 
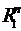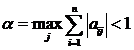, Rn: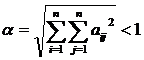 
.
При виконанні однієї з трьох умов стиску, розв’язок системи можна знайти за теоремою Банаха. За нульове наближення можна прийняти стовпець вільних членів: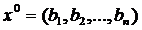 
. Підставивши його у систему отримаємо перше наближення. Продовжуючи цей процес отримаємо послідовність наближень, яка прямує до точного розв’язку. Для того щоб отримати наближення з певною точністю користуються оцінкою: 
.
|
|
|
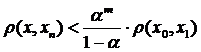Застосування теореми Банаха для доведення існування і єдності розв’язку задачі Коші диференціального рівняння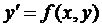 
.
Нехай маємо диференціальне рівняння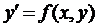 
. Відомо, що воно має безліч розв’язків, які залежать від деякого параметра с. Розв’язок, який задовольняє початковій умові 
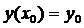називається частковим. Відшукання часткового розв’язку такого диференціального рівняння звуть задачею Коші. Розв’язати її важко, інколи точно взагалі неможливо. Тоді розв’язують наближено. Але при цьому треба бути впевненим, що розв’язок існує і єдиний. Це доводиться за допомогою теореми Банаха.
Теорема. Нехай маємо рівняння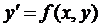 
з початковою умовою 
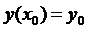, де функція 
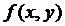– визначена і неперервна в деякій області 
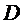, що містить точку (x0,y0), і задовольняє в цій області умову Ліпшиця по змінній y: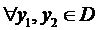 
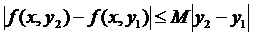. Тоді існує такий сегмент 
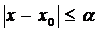на якому існує єдина функція 
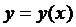, яка є розв’язком вихідного рівняння і задовольняє початкову умову.
|
|
|
Доведення. Спочатку доведемо еквівалентність вихідного диференціального рівняння з початковою умовою та інтегрального рівняння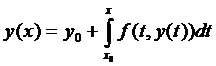 
.
Нехай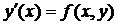 
, 
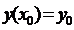, (1).
Проінтегруємо це рівняння в межах від x0 до x, вважаючи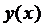 
неперервною.
;
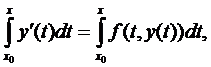
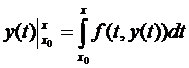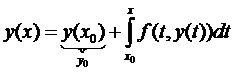(2).
Тепер нехай y(x) є розв’язком рівняння (2). Оскільки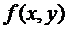 
– неперервна і y(t) – неперервна, то їх суперпозиція також є неперервною. Тоді можемо взяти похідну від інтеграла з верхньою змінною межею, і отримаємо: 
, 
.
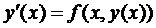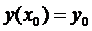Доведемо існування розв’язку інтегрального рівняння. Оскільки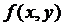 
неперервна в 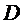, то буде неперервною і в деякій замкненій 
, 
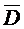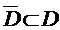. Тоді за теоремою Вейєрштрасса 
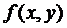буде обмеженою деяким числом k в : 
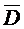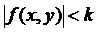. Підберемо 
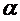, яке фігурує в умові теореми, так щоб:
1) 
, 
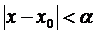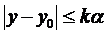, то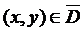 
2) 
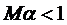, М – константа з умови Ліпшиця.
Розглянемо простір C*, елементами якого є неперервні функції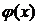 
на сегменті 
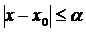, які задовольняють умову 
.
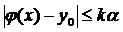Розглянемо в цьому просторі C* оператор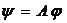 
, 
.
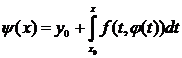Покажемо, що до цього оператора може бути застосована теорема Банаха, яка забезпечує існування нерухомої точки цього оператора, або що те саме розв’язку інтегрального рівняння (2), а отже і еквівалентного йому рівняння (1). Перевіримо виконання умов теореми Банаха.
|
|
|
1. Простір C* – повний, як замкнений підпростір повного простору С[a,b] .
2. Маємо відображення в себе, дійсно: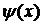 
– неперервна, як суперпозиція неперервних функцій. Крім того:
.
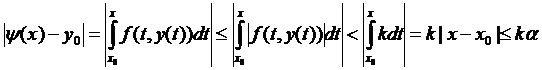3. Перевіримо умову стиску:
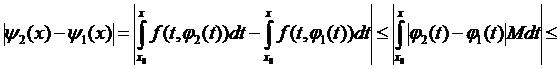
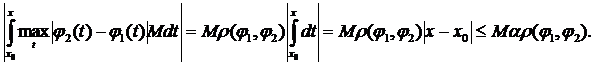
Нерівність виконується для всіх x, то і для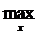 
теж: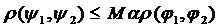 
. В припущенні, що 
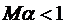, умова стиску виконується. Всі три умови теореми Банаха виконуються, отже існує нерухома точка оператора 
.
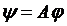Зауваження. В умові теореми фігурує умова Ліпшиця, її важко перевірити на практиці, тому замінюють простішою, а саме вимагають, щоб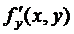 
була неперервною, тоді за теоремою Веєрштрасса 
; 
,
.
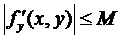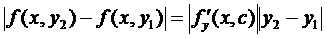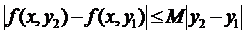Зауваження. В цьому методі наближений розв’язок наближається до точного розв’язку із швидкістю геометричної прогресії. Тут справедлива оцінка:
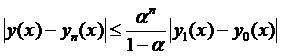, для, будь-якого x. Крім того, в процесі обчислень не накопичуються похибки.
Дата добавления: 2018-04-15; просмотров: 472; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!