Зв’язність та її збереження при неперервному відображенні.

Означення. Множина Е називається зв’язною, якщо її не можна подати у вигляді об’єднання двох відкритих множин, що не перетинаються.

Теорема. Образ зв’язної множини при неперервному відображенні є множина зв’язна.

Доведення. Дано 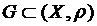 – зв’язна. Треба довести  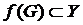– зв’язна. Нехай  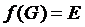– не зв’язна, і її подано у вигляді об’єднання двох відкритих множин, які не перетинаються. Позначимо їх через Е₁ та Е₂. Але за критерієм неперервності прообраз множини Е₁ – відкрита множина, і прообраз Е₂– також відкрита. Позначимо їх G₁  та G₂ , вони не будуть перетинатися (в силу неперервності відображення). Тобто множину праобразів ми подали у вигляді об’єднання двох відкритих множин, що не перетинаються , а це суперечить тому, що G – зв’язна. Отже образ  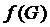– є множина зв’язна.

Теорему доведено.

 

Контрольні запитання.

1. Дати означення відображення множини 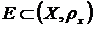 у простір .

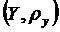2. Дати означення неперервності відображень та гомеоморфізму.

3. Сформулювати критерій неперервності.

4. Сформулювати теорему про зв’язність образу при неперервному відображенні.

5. Дати означення рівномірної неперервності відображення.

 

Вправи.

1. Навести приклади відображень з простору  R¹ в R¹; з R² в R¹; з С_[a,b]  в R¹; з С_[a,b]  в С_[a,b] .

2. Дано оператор Фредгольма 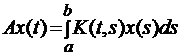, причому всі функції, які тут фігурують неперервні на замкнених множинах. Довести неперервність даного відображення.

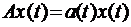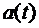3. Чи буде неперервним відображення А простору C_[0,1] в себе, що діє за формулою , де  – задана неперервна функція.

4. Дана функція 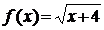. Довести на мові “ 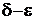” неперервність функції в точці х=5.

 

Розв’язання.

1. Прикладами таких відображень можуть бути відображення: 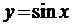, , 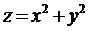, , 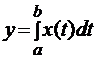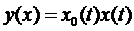де 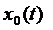 – фіксована функція, а  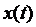– довільна.

2. Доведемо неперервність відображення за Гейне, тобто на мові послідовностей. Нехай маємо послідовність неперервних функцій 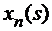, які прямують до x(s) в тому розумінні, що 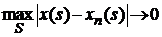, при 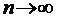. Тоді

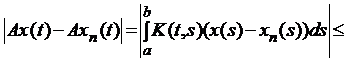
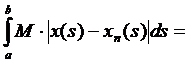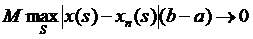 = , при , .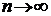

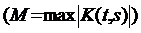Неперервність відображення доведена.

3. Дане відображення буде неперервним. В цьому можна переконатись точно так само, як це було зроблено в попередньому прикладі.

4. В точці х=5 функція визначена: 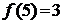. Задамо 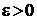. Складемо різницю 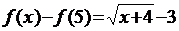, оцінимо її за модулем. При  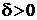для значень х, які задовольняють нерівності 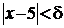, буде також виконуватись нерівність:

.

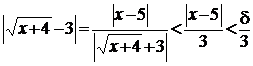Якщо тепер покласти 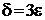, то при значеннях х, для яких 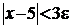, буде виконуватись нерівність .

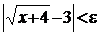Неперервність функції при х=5 доведена.

 

Задачі.

1. Навести приклади відображень: R¹ в R¹; з Rⁿ в R¹; з Rⁿ в Rⁿ; з С_[a,b]  в R¹; з С_[a,b]  в С_[a,b] ; з R¹ в Rⁿ.

2. Довести за означенням на мові “ 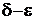” неперервність функції в точці x₀.

3. Довести що функції у=х і у=sinx рівномірно неперервні на всій числовій осі.

4. Довести, що функція 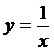 неперервна на інтервалі 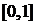, але не є рівномірно неперервною на цьому проміжку.

5. Навести приклад неперервного відображення, яке не є гомеоморфізмом.

6. Довести неперервність числової функції 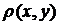 в будь-якому метричному просторі.

7. Довести неперервність векторної функції 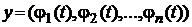 числового аргументу t, якщо координатні функції  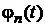неперервні.

8. Довести неперервність відображення:

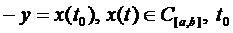 – фіксована точка сегменту .

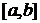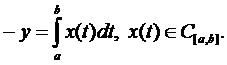
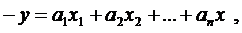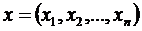 де  – довільний вектор,

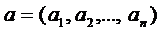 – фіксований вектор.

– ;

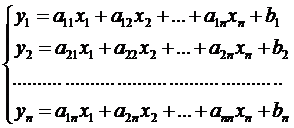Тут матриця коефіцієнтів 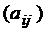 і стовпець вільних членів (b_s), (i=1,2,...,n) задані,  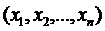змінний довільний вектор x.

 

ПОВНОТА МЕТРИЧНИХ ПРОСТОРІВ

В математичному аналізі фундаментальну роль відіграє критерій Коші збіжності числової послідовності (для того щоб послідовність була збіжна необхідно і достатньо щоб вона була фундаментальна). Цей критерій характеризує повноту метричного простору R , або числової прямої (на числовій осі немає дірок). Але цей критерій перестає бути справедливим в довільному просторі.

Приклад. Дійсно нехай маємо проміжок (0,1). Відстань задамо так: 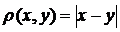. Розглянемо послідовність: 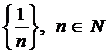. Очевидно, що при 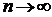, границею нашої послідовності буде нуль, але нуль не належить нашому простору.

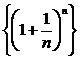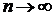Розглянемо інший приклад: множину раціональних чисел і послідовність , при  границею цієї послідовності буде число е, яке є ірраціональним.

Означення. Метричний простір 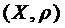 називається повним, якщо будь-яка фундаментальна послідовність в цьому просторі має границю.

Приклад. Дослідимо на повноту простір 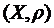, , 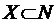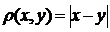. Розглянемо довільну фундаментальну послідовність складену із елементів такого простору. Такою послідовністю тут може бути така послідовність: скінчена кількість перших n членів послідовності буде довільними елементами, а починаючи з (n+1)-го, якийсь один із елементів повторюватиметься (інших випадків не може бути). Границею такої послідовності буде очевидно елемент, що повторюватиметься, він належатиме простору N, отже такий простір повний за означенням.

В математичному аналізі важливу роль відіграє теорема Кантора про систему вкладених і стискуючих сегментів, довжини яких прямують до нуля, яка стверджує, що така система має одну спільну точку. Цей факт виражає факт повноти числової прямої. Аналогічну роль відіграє теорема про вкладені одна в одну кулі.

Теорема 1. Будь-яка система вкладених одна в одну замкнених куль радіуси, яких прямують до нуля, мають в повному метричному просторі не порожній перетин.

Доведення. Дано:

1) Послідовність вкладених куль B₁(x₁,r₁)ÉB₂(x₂,r₂)É…ÉB_n(x_n,r_n)É…,

2) Кулі 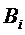 – замкнені,

3) ,

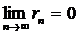4)  Простір повний.

Довести, що кулі мають не порожній перетин. Розглянемо послідовність центрів куль х₁,х₂,…,х_n. Ця послідовність буде фундаментальною. Справді, при n® 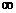 і m>n,  r(x_n,x_m)<r_n ® 0, що означає фундаментальність. В силу повноти простору ця послідовність має границю 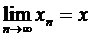. Покажемо що х належить всім кулям. Дійсно, х є граничною точкою для кожної кулі, бо в будь-якому її околі міститься нескінченна кількість точок кожної з куль. В силу замкненості куль, х належатиме кожній кулі, а значить належить перетину.

Теорема 2. Замкнений підпростір повного простору повний.

Доведення. Дано (Х,r) – повний простір і (Y,r)Ì(Х,r) – замкнений. Довести (Y,r) – повний. Розглянемо довільну фундаментальну послідовність {у_n}Ì(Y, r)Ì(Х, r). Простір (Х,r) – повний простір, отже ця послідовність має в ньому границю: 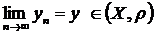. Але у – гранична точка множини  (Y, r), а (Y, r) – замкнений, значить містить всі свої граничні точки, .

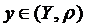Теорему доведено.

 

---

Дата добавления: 2018-04-15; просмотров: 401; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!