Застосування теореми Банаха для доведення існування задачі Коші нормальної системи диференціальних рівнянь.

Система виду:

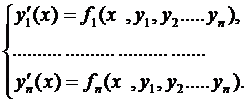(1)

називається нормальною системою диференціальних рівнянь. Тут кожне рівняння розв’язане відносно похідної. Маємо n рівнянь з n невідомими функціями 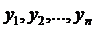. Нехай маємо початкові умови:

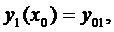
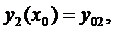(1*)

……………

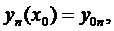
Система функцій 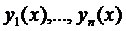на деякому проміжку зміни x називаються розв’язком системи (1), якщо при підстановці в цю систему ми одержимо тотожності.

Відшукання розв’язків 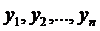, які задовольняють умови (1*) називається задачею Коші. Розв’язати цю задачу важче ніж попередню.

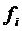
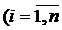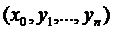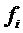Теорема. Нехай маємо нормальну систему диференціальних рівнянь виду (1) з умовами (1*), де функції ) визначені і неперервні в просторі Rⁿ⁺¹, який містить точку , і задовольняють умову Ліпшиця у формі

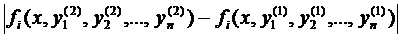
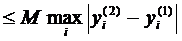, M>0. Тоді існує сегмент 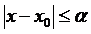, на якому існують функції 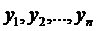, які є розв’язками нормальної системи (1) і задовольняють (1*).

Схема доведення. Аналогічно до попередньої теореми, спочатку замінюємо нормальну систему диференціальних рівнянь з початковими умовами еквівалентною системою інтегральних рівнянь:

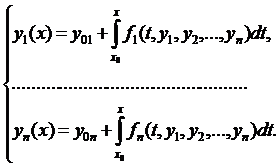
Введемо оператор 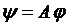, який розписують так:

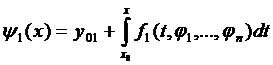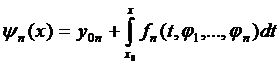,…, , який набору функцій 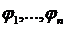ставить у відповідність 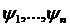. Набір функцій 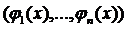визначений на деякому сегменті 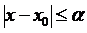, належать деякому підпростору неперервних функцій. Далі застосуємо до оператора теорему Банаха. Для цього переконаємось, що виконується три умови теореми:

1. Підпростір, на якому задані функції 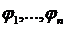повний, як замкнений підпростір повного простору.

2. Доводимо, що тут є відображення в себе.

3. Доводимо, що маємо оператор стиску.

Таким чином за теоремою Банаха існує нерухома точка даного оператора, тобто існує такий набір функцій 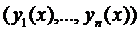, образом якого є такий же набір функцій 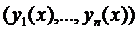, а це означає, що система інтегральних рівнянь має єдиний розв’язок, а саме 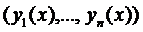. Тоді і вихідна система диференціальних рівнянь теж має єдиний розв’язок, який задовольняє початковим умовам.

Застосування теореми Банаха до розв’язання інтегральних рівнянь Фредгольма ІІ-го роду.

Інтегральним рівнянням Фредгольма ІІ-го роду назвемо рівняння виду 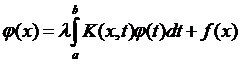, де 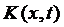– ядро, неперервна в деякому замкненому прямокутнику 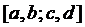функція (відома), 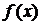– вільний член, неперервна функція, 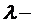параметр (дійсне чи комплексне число), 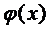– неперервна невідома функція.

Знайдемо 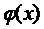методом послідовних наближень. Розглянемо оператор .

, , .

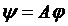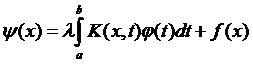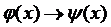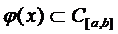Перевіримо умови теореми Банаха:

1) Простір неперервних функцій заданих на 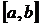є повним.

2) Маємо відображення в себе.

3) .

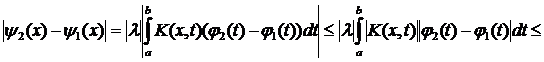
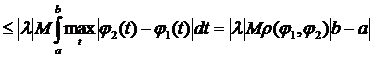Оскільки 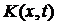неперервна в замкненому прямокутнику, то за теоремою Вейєрштрасса вона є обмежена, тобто 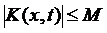. Нерівність має місце 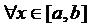, отже виконується і для максимального. 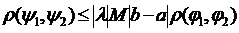. Вимагатимемо, щоб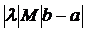 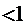, щоб виконувалася умова стиску. Підберемо 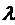, так щоб .

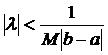Дата добавления: 2018-04-15; просмотров: 405; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!