ЛІНІЙНІ, НОРМОВАНІ ТА ЕВКЛІДОВІ ПРОСТОРИ
Лінійні простори.
Поняття лінійного простору належить до основних у функціональному аналізі.
Означення. Множина елементів довільної природи  називається лінійним простором якщо:
називається лінійним простором якщо:
1. На цій множині визначена операція додавання елементів, яка двом елементам x і y ставить у відповідність третій елемент z, який називають сумою.  ,
,  і виконуються властивості:
і виконуються властивості:
а)  – комутативність.
– комутативність.
б)  – асоціативність.
– асоціативність.
в)  .
.
г)  .
.
2. Визначена операція множення на число  (дійсне або комплексне)
(дійсне або комплексне) 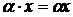 і виконуються властивості:
і виконуються властивості:
а)  – асоціативність;
– асоціативність;
б)  ;
;
в)  – розподільний закон;
– розподільний закон;
г)  – розподільний закон.
– розподільний закон.
Приклади.
1.  лінійний простір.
лінійний простір.
2.  :
:  ,
,
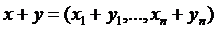 ,
,  .
.
3. 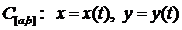 ;
;  ;
;  .
.
Введемо поняття лінійної залежності і лінійної незалежності елементів.
Означення. Елементи довільної природи 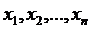 називаються лінійно залежними, якщо існує набір чисел
називаються лінійно залежними, якщо існує набір чисел  , серед яких хоч одне відмінне від нуля, що виконується рівність
, серед яких хоч одне відмінне від нуля, що виконується рівність  .
.
Факт лінійної залежності означає, що один із елементів можна виразити як лінійну комбінацію інших елементів:
 ,
,  .
.
Означення. Елементи  звуться лінійно незалежними, якщо рівність
звуться лінійно незалежними, якщо рівність  , має місце тоді і тільки тоді, коли всі
, має місце тоді і тільки тоді, коли всі  ,
,  .
.
Приклад.
Дослідити на лінійну залежність функцій:
1)  ,
,  , 5
, 5  . Маємо:
. Маємо:  , тобто функції лінійно залежні.
, тобто функції лінійно залежні.
2) 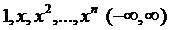 ;
;  ; Незалежні.
; Незалежні.
В лівій частині алгебраїчний многочлен n-того степеня. Має  коренів, а нам потрібною щоб він був рівний нулю для будь-якого x. Це можливо тільки тоді, коли всі
коренів, а нам потрібною щоб він був рівний нулю для будь-якого x. Це можливо тільки тоді, коли всі  .
.
|
|
|
Означення. Лінійний простір зветься n-вимірним, якщо в ньому існує n лінійно незалежних елементів, а будь-які (  ) елементів вже лінійно залежні.
) елементів вже лінійно залежні.
Ці n лінійно незалежних елементи звуть базисом даного простору.
 :
:  – базис.
– базис.
Означення. Лінійний простір звуть нескінченно вимірним, якщо в ньому існує як завгодно велика кількість лінійно незалежних елементів. Скінченно вимірні простори вивчаються в лінійній алгебрі, а нескінченно вимірні в функціональному аналізі.
1.  :
:  ,
, 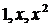 ,…,
,…,  … – базис
… – базис
2. 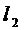 :
:  ,
, 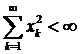 ;
;  – базис .
– базис .
Означення. Підпростором L* лінійного простору L називається множина елементів з простору L, якщо з того, що x і y 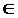 L* випливає, що
L* випливає, що  , при всіх
, при всіх  і
і  .
.
Всякий простір L містить підпростір самого себе і нуль простір. Підпростір який не співпадає з L і нуль підпростором зветься власним підпростором L.
Нехай маємо деяку множину 
 . Лінійною оболонкою даної множини називається найменший лінійний підпростір з простору L, який містить елементи множини
. Лінійною оболонкою даної множини називається найменший лінійний підпростір з простору L, який містить елементи множини  .
.
Нормовані простори.
У функціональному аналізі приходиться мати справу з просторами, які є одночасно лінійними і метричними. До таких просторів належать нормовані простори. Нехай маємо лінійний простір L.
|
|
|
Означення. Простір L зветься нормованим, якщо кожному елементу x 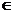 L поставлено у відповідність число
L поставлено у відповідність число  – норма x, яке задовольняє аксіомам:
– норма x, яке задовольняє аксіомам:
1.  ;
;
2.  ,
,  , R – дійсні, C– комплексні;
, R – дійсні, C– комплексні;
3.  .
.
Інтерес до цих просторів викликаний тим, що їх легко метризувати, тобто ввести поняття відстані  .
.
1.  ;
; 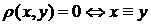 ;
;
2.  ;
;
3.  .
.
Норма елемента x – це відстань між ним і нульовим елементом  .
.
Приклади.
1. Rn, 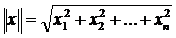 ;
;
2. l2, 
 ,
, 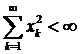 – збіжний;
– збіжний;
3.  ,
,  ,
,  .
.
Означення. Повні нормовані простори звуться просторами Банаха.
Евклідові простори.
Розглянемо  простір Rn, його елементами є набори дійсних чисел
простір Rn, його елементами є набори дійсних чисел 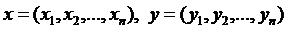 .
.
Скалярним добутком двох векторів називається число  .
.
У довільному лінійному абстрактному просторі поняття скалярного добутку означається аксіоматично. Нехай маємо деякий лінійний простір L.
Означення. Число  зветься скалярним добутком двох елементів, якщо воно задовольняє наступним аксіомам:
зветься скалярним добутком двох елементів, якщо воно задовольняє наступним аксіомам:
1.  ;
;
2. 
 – число;
– число;
3.  ;
;
4.  ,
,  .
.
Означення. Лінійний простір з фіксованим в ньому скалярним добутком зветься евклідовим.
Приклади.
1. l2,  . Збіжність ряду випливає з очевидної нерівності
. Збіжність ряду випливає з очевидної нерівності  .
.
2.  ,
,  ,
,  .
.
Виконання всіх аксіом скалярного добутку випливає з властивостей визначеного інтеграла.
|
|
|
1.  ;
;
2.  ;
;
3.  ;.
;.
4.  . Якщо
. Якщо  , то
, то  ; Нехай
; Нехай  , доведемо, що
, доведемо, що  . Нехай існує точка
. Нехай існує точка  , у якій
, у якій  , тоді в силу неперервності функція
, тоді в силу неперервності функція  буде більшою нуля і в деякому околі
буде більшою нуля і в деякому околі  . Тоді
. Тоді  . Суперечність.
. Суперечність.
Евклідів простір можна зробити нормованим поклавши  . Щоб довести це доведемо спочатку лему Коші-Буняковського.
. Щоб довести це доведемо спочатку лему Коші-Буняковського.
Лема. В евклідовому просторі має місце нерівність:  .
.
Доведення. Використаємо функцію  ,
,

Отримали квадратний тричлен відносно параметра 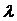 .
.
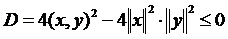 ;
;  ;
;  .
.
Розглянувши конкретні простори Rn і  , та знайшовши в них скалярний добуток, норми x та y, ми отримаємо дві відомі нам класичні нерівності Коші-Буняковського. Далі перевіримо виконання аксіом норм.
, та знайшовши в них скалярний добуток, норми x та y, ми отримаємо дві відомі нам класичні нерівності Коші-Буняковського. Далі перевіримо виконання аксіом норм.
1.  ,
,  ;
;
2.  ;
;
3. 

Добувши корінь квадратний із обох частин отримаємо:  . Нерівність Коші-Бунявського дозволяє ввести поняття косинуса кута між двома абстрактними елементами
. Нерівність Коші-Бунявського дозволяє ввести поняття косинуса кута між двома абстрактними елементами  .
.
Два елементи x та y з евклідового простору будемо вважати ортогональними, якщо їх скалярний добуток рівний нулеві.
Означення. Система елементів  із Евклідового простору зветься ортогональною, якщо:
із Евклідового простору зветься ортогональною, якщо:  при
при 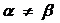 ;
;  при
при  . Якщо
. Якщо  , то така система зветься ортонормованою.
, то така система зветься ортонормованою.
Можна довести, що коли система ортонормована, то вона лінійно незалежна, тобто, що 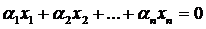 тоді і тільки тоді, коли
тоді і тільки тоді, коли  . Дійсно розглянемо скалярний добуток
. Дійсно розглянемо скалярний добуток
|
|
|
 ,
,  ;
;  ,
,  ;
;
Означення. Ортогональна система елементів евклідового простору L називається ортогональним базисом цього простору, якщо найменший лінійний підпростір, який містить ортогональну систему співпадає з усім простором L.
Ортонормована система функцій називається повною в деякому просторі, якщо будь-який елемент x  з цього простору можна як завгодно точно наблизити лінійною комбінацією базисних векторів у розумінні норми даного простору.
з цього простору можна як завгодно точно наблизити лінійною комбінацією базисних векторів у розумінні норми даного простору.
Контрольні запитання.
1. Дати означення лінійного простору. Навести приклади.
2. Який лінійний простір називається n-вимірним? Нескінченно вимірним?
3. Дати означення лінійного многовиду.
4. Дати означення норми та нормованого простору.
5. Дати означення скалярного добутку та евклідового простору.
6. Записати нерівність Коші-Буняковського в евклідовому просторі.
7. Дати означення ортонормованого базису в евклідовому просторі.
8. Сформулювати теорему про ортогоналізацію.
9. Записати нерівність Бесселя та рівність Парсеваля.
Вправи.
1. Розглянемо множину  усіх прямокутних матриць порядку
усіх прямокутних матриць порядку  із скалярними елементами
із скалярними елементами


Означимо в  операції
операції  Довести, що
Довести, що  є лінійний простір.
є лінійний простір.
2. Покладемо в нормованому просторі 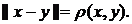 Перевірити виконання аксіом так означеної метрики.
Перевірити виконання аксіом так означеної метрики.
3. Нехай 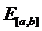 – лінійний простір усіх дійсних функцій, визначених на сегменті
– лінійний простір усіх дійсних функцій, визначених на сегменті  Довести, що простір
Довести, що простір  – неперервних функцій на сегменті
– неперервних функцій на сегменті  є лінійним многовидом .
є лінійним многовидом .
4. У просторі  означемо скалярний добуток за формулою
означемо скалярний добуток за формулою
 Перевірити виконання аксіом скалярного добутку.
Перевірити виконання аксіом скалярного добутку.
Розв’язання.
Оскільки операції над матрицями зводяться до виконання операцій над числами, то справедливість аксіом лінійного простору очевидна.
1. Перевіримо виконання аксіом метрики, враховуючи виконання аксіом норми.
a)  причому
причому  тоді, і тільки тоді, коли
тоді, і тільки тоді, коли  .
.
b) 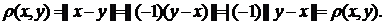
c) 
2. Це випливає з відомого з математичного аналізу факту, що лінійна комбінація двох неперервних на сегменті  функцій є функція неперервна на цьому відрізку.
функцій є функція неперервна на цьому відрізку.
3. Перевіримо виконання аксіом скалярного добутку.  , причому
, причому  тоді і тільки тоді, коли
тоді і тільки тоді, коли 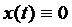 . Справді, якщо
. Справді, якщо  то
то 
Якщо ж  , то звідси випливає, що
, то звідси випливає, що  , коли б
, коли б  хоча б в одній точці
хоча б в одній точці  , то в силу неперервності функція x(t) була б, наприклад, більшою від нуля і в деякому колі точки
, то в силу неперервності функція x(t) була б, наприклад, більшою від нуля і в деякому колі точки  , а тоді не виконувалася б рівність
, а тоді не виконувалася б рівність 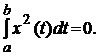
Виконання трьох інших аксіом скалярного добутку випливає з властивостей визначеного інтеграла.
Задачі.
1. У просторі  і
і 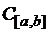 операції додавання елементів і множення елемента на число введені за формулами:
операції додавання елементів і множення елемента на число введені за формулами:
а) 
б) 
Перевірити лінійність просторів  і
і  .
.
2. Покажіть, що в  функції
функції  лінійно незалежні, а функції
лінійно незалежні, а функції  лінійно залежні.
лінійно залежні.
3. Довести, що простори  нескінченно вимірні.
нескінченно вимірні.
4. Покажіть, що множна всіх многочленів степеня не вищого за 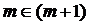 – є вимірним лінійним многовидом в
– є вимірним лінійним многовидом в 
5. Покажіть, що в  множина всіх функцій, які задовольняють граничним умовам
множина всіх функцій, які задовольняють граничним умовам  , буде лінійним многовидом тоді і тільки тоді, коли
, буде лінійним многовидом тоді і тільки тоді, коли  .
.
6. У просторах  норми елементів означені за формулами:
норми елементів означені за формулами: 
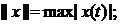
 відповідно. Перевірити виконання аксіом норм.
відповідно. Перевірити виконання аксіом норм.
7. Довести нерівність Коші-Буняковського в евклідовому просторі.
8. У просторі  скалярний добуток означимо за формулою
скалярний добуток означимо за формулою  Доведіть, що ряд
Доведіть, що ряд  – збіжний і виконується аксіома скалярного добутку. Як виглядає в
– збіжний і виконується аксіома скалярного добутку. Як виглядає в  множина ортогональних елементів.
множина ортогональних елементів.
Дата добавления: 2018-04-15; просмотров: 1710; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
