Общая постановка задачи устойчивости по А.М. Ляпунову
А. М. Ляпуновым было дано следующее определение устойчивости: невозмущенное движение называют устойчивым по отношению к переменным 
если при всяком произвольно заданном положительном числе ε, как бы мало оно ни было, можно выбрать другое такое положительное число δ(ε), что при всяких возмущениях xi0, удовлетворяющих условию
(3.13)
и при любом t≥ t0 будет выполняться неравенство
(3.14)
в противном случае движение неустойчиво.
Геометрическая интерпретация этого условия заключается в следующем. В пространстве координат xi построим две сферы с радиусами δи ε (ε > δ). Система будет устойчивой, если при возмущениях, не выведших изображающую точку 
из пределов сферы δ, возмущенное движение будет таково, что, начиная с некоторого времени t ≥ T , изображающая точка 
будет в пределах сферы ε.
Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения. Если невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.
Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, т. е.
, (3.15)
то невозмущенное движение называют асимптотически устойчивым.При асимптотической устойчивости изображающая точка с течением времени должна неограниченно стремиться к началу координат.
|
|
|
Некоторые особенности определения устойчивости по А. М.Ляпунову:
· предполагают, что возмущения налагаются только на начальные условия, иначе говоря, возмущенное движение происходит при тех же силах (источниках энергии), что и невозмущенное движение.
· устойчивость рассматривают на бесконечно большом промежутке времени.
· возмущенияпредполагаются малыми.
Теорема А.М. Ляпунова об устойчивости движения по первому приближению.
Чтобы вывести уравнения возмущенного движения, найдем из (3.9) переменные 
и подставим эти значения 
в дифференциальные уравнения движения (3.2). Тогда
(3.16)
Если правые части уравнений (3.16) допускают разложение в степенные ряды Тейлора, то после этого разложения по степеням получим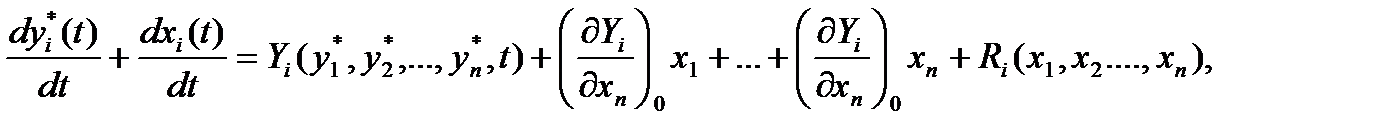 
(3.17)
где 
— совокупность членов, зависящих от отклонений в степени выше первой. Учитывая (4), будем иметь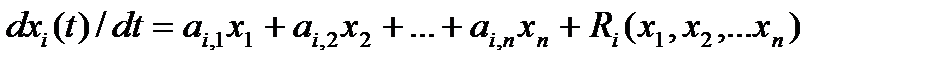 
. (3.18)
Если отклонения достаточно малы, то, пренебрегая 
,
|
|
|
получимлинеаризованные уравнения называемые уравнениями первого приближения:
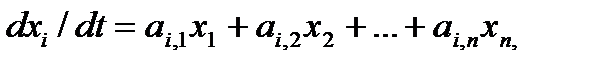, i = 1,2,…n, (3.20)
Системе уравнений (3.20) соответствует характеристическое уравнение, которое можно записать следующим образом:
Из (3.21) можно найти его корни 
, где i= 1, 2, ..., n, которые в общем случае имеют вид, где 
и 
— вещественные и мнимые части корней соответственно.
Теорема 1. Если вещественные части всех корней характеристического уравнения (3.21)первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.
Теорема 2. Если среди корней 
характеристического уравнения (3.21)первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.
Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Как показал Ляпунов, в критическом случае устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, так как она зависит от вида нелинейной функции 
,
Дата добавления: 2018-04-05; просмотров: 423; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!