Уравнения динамики и статики

На определенном этапе разработки и исследования автоматической систе­мы управления получают ее математи­ческое описание — описание процессов, проистекающих в системе, на языке ма­тематики. Математическое описание мо­жет быть аналитическим (с помощью уравнений), графическим (графики, структурные схемы и графы) и табличным (с помощью таблиц).

Для получения математического опи­сания системы обычно составляют опи­сание ее отдельных элементов. В част­ности, для получения уравнений систе­мы составляют уравнения для каждого входящего в нее элемента. Совокупность всех уравнений элементов и дает урав­нения системы.

Уравнения (а также структурные схе­мы) автоматической системы управле­ния называют ее математической мо­делью. Такое название обусловлено тем, что при математическом описании (сос­тавлении уравнений) физических про­цессов всегда делают какие-либо допу­щения и приближения.

Математическая модель одной и той же системы в зави­симости от цели исследования может быть разной. Более того, иногда полез­но при решении одной и той же задачи на разных этапах принимать разную ма­тематическую модель: начать исследова­ние с простейшей модели, а затем ее постепенно усложнять, с тем, чтобы учесть дополнительные явления и связи, которые на начальном этапе были отброшены как несущественные. Сказанное обусловливается тем, что к математической модели предъявляются противоречивые требования: она должна, с одной стороны, как можно полнее отражать свойства ори­гинала, а с другой стороны, быть по возможности простой, чтобы не усложнять исследование.

Система управления и любой ее элемент производят преоб­разование входного сигнала х(t)в выходной сигнал у(t). С математической точки зрения они осуществляют отображение

y(t) = Ax(t) (2.1)

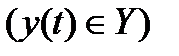согласно которому каждому элементу х(t)из множества Xвходных сигналов ставится в соответствие единст­венный, вполне определенный элемент у(t) из множества Y вы­ходных сигналов . В приведенном соотношении А называется оператором.Оператор, определяющий соответст­вие между входным и выходным сигналами системы управле­ния (элемента), называется операторомэтой системы(эле­мента). Задать оператор системы — это значит задать правило определения выходного сигнала этой системы по ее входному сигналу.

Рассмотрим математическое описание непрерывных систем управления с помощью дифференциальных уравнений. В боль­шинстве случаев звенья и системы описываются нелинейными дифференциальными уравнениями произвольного порядка. Здесь под звеном понимается математическая модель элемен­та. Для примера рассмотрим звено (рис.2.1), которое можно описать дифференциальным уравнением второго порядка

,                (2.2)

гдеу— выходная величина; uи f — входные величины; у′ и u′ — первые производные по времени; у″— вторая производ­ная по времени.

u

y

f

Рис.2.1. Структурная схема звена.

 

Уравнение (1), описывающее процессы в звене при про­извольных входных воздействиях, называют уравнением ди­намики. Пусть при постоянных входных величинах и процесс в звене с течением времени установится: выходная величина примет постоянное значение . Тог­да (1) примет вид

                                           (2.3)

Это уравнение описывает статический или установившийся режим и его называют уравнением статики.

Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена или элемента (а также системы) называют зависимость выходной величины от входной в статическом режиме. Стати­ческую характеристику можно построить экспериментально, подавая на вход элемента постоянное воздействие и измеряя выходную величину после окончания переходного процесса, или расчетным путем, используя уравнение статики.

Если звено имеет несколько входов, то оно описывается с помощью семейства или семейств статических характеристик. Например, звено, характеризующееся в статическом режиме уравнением (2.3), можно описать графически с помощью семей­ства статических характеристик, представляющих собой кри­вые зависимости выходной величины уот одной входной вели­чины u(или f) при различных фиксированных значениях дру­гой — f (или u).

 

Преобразование Лапласа.

Преобразованием Лапласа называется соотношение:

,                             (2.17)

ставящее функции X(t) вещественного переменного в соответствие функции X(s) комплексного переменного. При этом X(t) называется оригиналом, а X(s) изображением или изображением по Лапласу.

       Символические записи преобразования Лапласа

или ;

X(s)=L{X(t)},   L - оператор Лапласа.

Функция, которая подвергается преобразованию Лапласа, должна иметь следующие свойства:

1. X(t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [0;∞];
2. X(t)=0 при t < 0;
3. Существуют такие положительные числа М и C, что

, при 0 ≤ t< ∞.                  (2.18)

Функции, обладающие указанными свойствами, называются функциями-оригиналами.

Соотношение

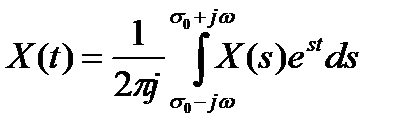,                                  (2.19)

называется обратным преобразованием Лапласа. В нем интеграл решается вдоль любой прямой Res=σ₀>C.

Символическая запись обратного преобразования Лапласа:

.      

 

Свойства преобразования Лапласа

а) Свойство линейности. Для любых постоянных α и β выполняется равенство:

 

б) Дифференцирование оригинала. Если производная X(t) является функцией-оригиналом, то

, где ,

в) Интегрирование оригинала.

.       

г) Теорема запаздывания. Для любого положительного числа

д) Теорема о свертке (теорема умножения изображений). Если и  - оригиналы, а  и - их изображения, то

.   (2.29)

е) Теоремы о предельных значениях. Если X(t)- оригинал, а X(s)-его изображение, то

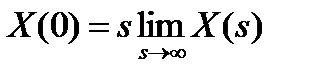(2.31)

       и при существовании предела

(2.32)

будет существовать предел

.

Передаточные функции.

При описании автоматических систем управления широко используют символическую форму записи линейных диффе­ренциальных уравнений. Рассмотрим ее на примере уравнения

                                 (2.48)

Введем для операции дифференцирования обозначение p_, т. е.

d/dt ≡ p;                                                                     (2.49)

(2.50)

  Используя его, уравнение(2.48) можно записать в виде:

Учитывая, что нельзя вместо руписать ур, перепишем (2.51), вынеся у и uзаскобки:   

(2.52)

Введем обозначения:  

 ,                               (2.53)

,                                           (2.54)

(2.55)

 С помощью этих обозначений урав­нение (2.53) можно записать в более компактной форме:

(2.56)

 

В уравнении (2.56)Q(р)(дифференциальный оператор при выходной величине) называют собственным оператором, а R₁(р)и R₂(р)(дифференциальные операторы при вход­ных величинах) — операторами воздействия. Отношение оператора воздейст­вия к собственному оператору называют передаточной функ­цией или передаточной функцией воператорной форме.

Звено, описываемое уравнением (2.48) или, что, то же самое, уравнениями    (2.49) — (2.56), можно характеризовать двумя пере­даточными функциями: передаточной функцией W₁(p)по входной величине uт. е.

,                (2.57)

и передаточной функцией W₂(р)по входной величине f, т.е.

(2.58)

Используя передаточные функции, уравнение (1) записы­вают в виде

(2.59)

Это уравнение представляет собой условную, более компакт­ную форму записи исходного уравнения (1).Уравнения (2.52),(2.56) и (2.59) называют уравнениями в символической или опе­раторной форме записи.

…

 

Частотные характеристики.

Важное значение при описании линейных стационарных си­стем (звеньев) имеют частотные характеристики. Они получа­ются при рассмотрении вынужденных движений системы (зве­на) при подаче на ее вход гармонического воздействия.

Длялинейных систем справедлив принцип суперпозиции, который можно сформулировать следующим образом: реак­ция системы на несколькоодновременно действующих входных воздействий равна сумме реакций накаждое воздействие в от­дельности. Это позволяет ограничиться изучением систем толь­ко с одним входом.

 В общем случае уравнение линейной ста­ционарной системы с одним входом можно записать так:

                (2.90)

Ее передаточная функция по определению:

(2.91)

Функцию W(jω), которую получают из передаточной функции (2.91) при подстановке в нее р = jω:

                    (2.92)

называютчастотной передаточной функцией. Частотная пере­даточная функция является комплексной функцией от действительной переменной ω, которая называется частотной. Функцию W(jω) можно представить в виде

,                 (2.93)

где

(2.94)

φ(ω) = argW(jω)                                                    (2.95)

 

Если

| argW(jω)| ≤ π/2,                                                (2.96)

то

(2.97)

Рис.2.5. Частотная передаточ­ная функция

На комплексной плоскости (рис. 2.5) частотная передаточ­ная функция W(jω) определяет вектор ОС,длина которого рав­на А(jω), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) —φ(ω). Кривую, которую описывает конец этого вектора при изменении часто­ты от 0 до ∞ (иногда от — ∞ до ∞), называют амплитудно-фазовойчастотной характеристикой (АФЧХ).

Частотную передаточную функцию будем называть также амплитудно-фазовой частотной функцией. Ее действительную часть U(ω) = ReW(ω) и мнимую часть V(ω) = ImW(ω) будем называть соответственно вещественнойи мнимой часто­тной функцией. График вещественной частотной функции [кри­вая зависимости U=U(ω)] называют вещественнойчастот­ной характеристикой, а график мнимой частотной функции — мнимойчастотной характеристикой. Модуль А (ω) = |W(ω) | называют амплитудной час­тотной функцией, ее гра­фик — амплитудной частот­ной характеристикой. Аргумент φ(ω)=argW(ω) называют фазовой частотной функцией, ее график — фа­зовой частотной характери­стикой.

 

 

 

---

Дата добавления: 2018-04-05; просмотров: 804; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!