Критерий устойчивости Михайлова
Пусть дано характеристическое уравнение системы:
 (3.87)
(3.87)
Левую часть характеристического уравнения называют характеристическим полиномом
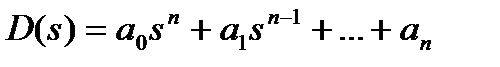 (3.88)
(3.88)
Если подставить в этот полином чисто мнимое значение s = jω, то получим комплексный полином
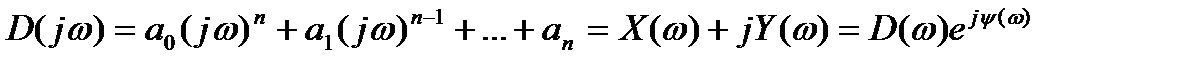 (3.89)
(3.89)
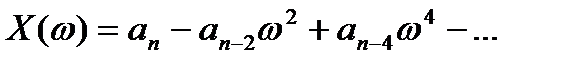 , (3.90)
, (3.90)
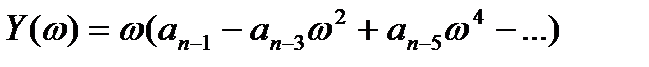 (3.91)
(3.91)
называют соответственно вещественной и мнимой функциями Михайлова; функции D(ω) и ψ(ω) представляют собой модуль и фазу (аргумент) вектора  .
.
При изменении частоты ω вектор  , изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.
, изменяясь по величине и направлению, будет описывать своим концом в комплексной плоскости некоторую кривую, называемую кривой (годографом) Михайлова.
В соответствии с (3.85) угол поворота вектора  вокруг начала координат при изменении частоты ω от 0 до ∞ равен:
вокруг начала координат при изменении частоты ω от 0 до ∞ равен:
|ω = ∞
ΔArg D(jω) = (π/2)(n-2m) (3.92)
|ω = 0
Отсюда определяем число правых корней полинома D(s), т. е.
 (3.93)
(3.93)
Из (3.93) видно, что число правых корней m будет равно нулю при одном-единственном условии
|ω = ∞
Δ Arg D(jω) = π n/2 (3.94)
|
|
|
|ω = 0
Условие (3.94) является необходимым, но не достаточным условием устойчивости. Для устойчивости системы необходимо и достаточно, чтобы все n корней характеристического уравнения были левыми; иначе говоря, среди них не должно быть корней, лежащих на мнимой оси и обращающих в нуль комплексный полином  , т. е. должно выполняться еще одно условие
, т. е. должно выполняться еще одно условие
D(jω) ≠ 0 (3.95)
Учитывая сказанное выше, критерий устойчивости Михайлова можно сформулировать так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты ω от 0 до ∞, начинаясь при ω = 0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно n квадрантов координатной плоскости, где n — порядок характеристического уравнения.
причем конец ее уходит в бесконечность в том квадранте координатной плоскости, номер которого равен степени характеристического уравнения.

Рис. 3.9. Типичные кривые Михайлова для устойчивых систем
|
|
|
Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости, вследствие чего угол поворота вектора  оказывается меньше, чем πn/2. Число правых корней неустойчивой системы можно определить по (3.93).
оказывается меньше, чем πn/2. Число правых корней неустойчивой системы можно определить по (3.93).
3.10 – неустойчивые системы

Рис. 3.10. Кривые Михайлова для неустойчивых систем.
Для границы устойчивости третьего типа (бесконечный корень)
конец кривой Михайлова перебрасывается как на рис. 3.11. При этом коэффициент  будет проходить через нуль, меняя знак плюс на минус.
будет проходить через нуль, меняя знак плюс на минус.

Рис. 3.11. Переход кривой Михайлова
В связи с указанным следствием можно привести другую формулировку критерия устойчивости Михайлова: система автоматического управления будет устойчива тогда и только тогда, когда вещественная X(ω) и мнимая Y(ω) функции Михайлова, приравненные нулю, имеют все действительные и перемежающиеся корни. Общее число этих корней равно порядку характеристического уравнения n, и при ω = 0 удовлетворяются условия
X(0) > 0, Y(ω) > 0 (3.99)
|
|
|
Пример. Определить устойчивость системы, характеристическое уравнение которой
 (3.100)
(3.100)
Подставляем s = jω и находим вещественную и мнимую функции Михайлова:
 (3.101)
(3.101)
 (3.102)
(3.102)
Находим корни уравнения Y(ω)=0:

 (3.103)
(3.103)
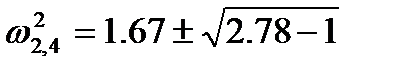 ,
,  ,
,  . (3.104)
. (3.104)
Если перемежаются корни, то перемножаются и их квадраты, поэтому нахождение ω2 и ω4 не обязательно.
Проверим, чередуются ли знаки X(ω) при подстановке  и
и 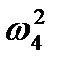 .
.
Имеем
 (3.105)
(3.105)
 (3.106)
(3.106)
Так как все корни Y(ω) вещественны и знаки ординат X(ω), соответствующие этим корням, чередуются, то система устойчива.
Дата добавления: 2018-04-05; просмотров: 649; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
