Элементарные звенья. Колебательное, консервативное, и апериодическое второго порядка
Звено, которое можно описать уравнением
 (2.177)
(2.177)
или
 , (2.178)
, (2.178)
гдеT=T0 , ξ=T1/(2T),
или передаточной функцией  , (2.179) называют
, (2.179) называют
· колебательным, если 0 <ξ < 1,
· консервативным, если ξ=0 (T1=0),
· апериодическим звеном второго порядка, если ξ ≥ 1.
Коэффициент ξ называют коэффициентом демпфирования.
Колебательное звено
Частотная передаточная функция:  . (2.180)
. (2.180)
Умножив числитель и знаменатель на комплексно – сопряженное знаменателю выражение, получим вещественную и мнимую частотные функции:
 ; (2.181)
; (2.181)
 (2.182)
(2.182)

Рис. 2.16. Характеристики колебательного звена.
а) Фазовая частотная функция, как это видно из АФЧХ (рис. а), изменяется монотонно от 0 до –π и выражается формулой:
1.  (2.183)
(2.183)
б) Логарифмическая фазовая частотная характеристика (рис. б) при ω → 0 асимптотически стремится к оси частот, а при ω → ∞ - к прямой φ = -π.
в) По переходной характеристике(рис.в)можно определить параметры колебательного звена следующим образом.Передаточный коэффициент определяют по установившемуся значению h(∞) переходной функции. Постоянную времени Т и коэффициент демпфирования ξ можно найти из уравнений  ;
;  , (2.190)где Тк – период колебаний; А1 и А2 – амплитуды двух соседних колебанийотносительно установившегося значения (рис. в).
, (2.190)где Тк – период колебаний; А1 и А2 – амплитуды двух соседних колебанийотносительно установившегося значения (рис. в).
| Амплитудная частотная функция |  , 2.184) , 2.184)
|
| Логарифмическая амплитудная функция | 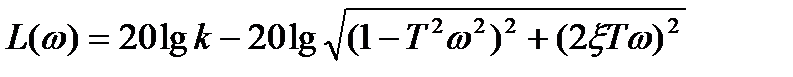 . (2.185) . (2.185)
|
| Уравнение асимптотической ЛАЧХ |  (2.186) (2.186)
|
Консервативное звено
|
|
|
Передаточная функция: 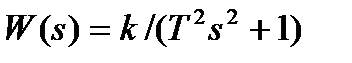 (2.191)
(2.191)
Частотная передаточная функция:  (2.192)
(2.192)

Рис. 2.17. Характеристики колебательного звена.
а) Фазовая частотная функция, как это следует из АФЧХ (рис. а)
0 при ω< 1/T
φ(ω)= -π при ω> 1/T (2.193)
Это выражение можно получить из фазовой частотной функции колебательного звена предельным переходом при ξ → 0. Нетрудно выписать выражения для остальных частотных функций;
б) ЛЧХ (рис. б)Сопрягающая частота:  (2.194)
(2.194)
в) Переходная функция  (2.195). Переходная характеристика (рис.в) представляет собой график гармонических колебаний с постоянной амплитудой.
(2.195). Переходная характеристика (рис.в) представляет собой график гармонических колебаний с постоянной амплитудой.
Апериодическое звено второго порядка (ξ ≥ 1)
Передаточную функцию (9) при ξ≥1 можно преобразовать к виду
 ,(2.196)
,(2.196)
где  . (2.197)
. (2.197)
Апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Оно неотносится к числу элементарных звеньев.
Элементарные звенья. Неминимально-фазовое, изодромное звенья.
Звено называют минимально – фазовым, если все нули и полюсы его передаточной функции имеют отрицательные или равные нулю вещественные части. Звено называют неминимально – фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.
|
|
|
Нулями передаточной функции W(s)=R(s)/Q(s), (2.198) где R(s) и Q(s) – полиномы от s, называют корни уравненияR(s)=0, т. е. такие значения s, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения Q(s)=0 т. е. такие значения s, при которых передаточная функция обращается в бесконечность.
Неминимально – фазовые звения
Все рассмотренные выше элементарные звенья относятся к минимально – фазовым. Примерами неминимально – фазовых элементарных звеньев являются звенья с передаточными функциями:
W(s)=k/(Ts-1) (2.199)
W(s)=k(Ts-1) (2.200)
 (2.201)
(2.201)
 (2.202)
(2.202)
Для неминимально – фазового звена характерно, что у него сдвиг фазы по модулю больше, чем у минимально – фазового звена, имеющего одинаковую с неминимально – фазовым звеном АЧХ. Нарис.2.18приведены ЛЧХ неминимально – фазовых звеньев с передаточными функциями W(s)=1/(Ts-1) (2.203)(рис. а) и W(s)=k(Ts-1) (2.204)(рис. б).
ЛАЧХ этих звеньев совпадают с ЛАЧХ апериодического и форсирующегозвеньев. Сдвиг фазы у последних меньше: фазовые частотные функции апериодического и форсирующего звеньев по абсолютной величине не превышают значения π/2, а фазовые частотные функции соответствующих неминимально – фазовых звеньев достигают по абсолютной величине значения π.
|
|
|

Рис.2.18. Характеристики неминимально – фазовых звеньев.
К неминимально – фазовым звеньям относят также звено чистогозапаздывания с передаточной функцией:
 (2.205)
(2.205)
Частотная передаточная функция:  (2.206)
(2.206)
Модуль частотной передаточной функцииA(ω) = k; (2.207)

Рис. 2.19. Характеристики звена чистого запаздывания
Амплитудно – фазовая частотная характеристика звена чистого звена запаздывания (рис.а). Это окружность с центром в начале координат и радиусом k:
U(ω) = kcosωτ (2.208)
V(ω) = - ksinωτ (2.209)
Каждой точке этой характеристики соответствует бесконечное множество значений частот. ЛАЧХ (рис.б) совпадает с ЛАЧХ пропорционального звена с передаточной функцией kL(ω) = 20lgk (2.210)
ЛФЧХ (рис. б):φ(ω) = - ωτ (2.211)
Переходная характеристика (рис.в):h(t) = k1(t-τ) (2.212)
Функция веса: w(t) = kδ(t-τ). (2.213)
|
|
|
Изодромные звенья
Изодромное звено первого порядка имеет следующие характеристики:
| передаточная функция: | W(s) = [k(τs+1)]/s; (2.214) |
| переходная характеристика: |  ; (2.215) ; (2.215)
|
| функция веса: |  (2.216) (2.216)
|

Рис. 2.20. Характеристики изодромного звена 1-го порядка
Изодромное звено второго порядка имеет следующие характеристики:
| передаточная функция: | 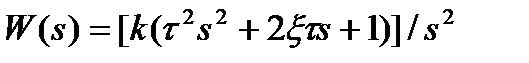 ; (2.217) ; (2.217)
|
| переходная характеристика: |  ; (2.218)
где: ; (2.218)
где:  , ,  ; (2.219) ; (2.219)
|
| функция веса: | 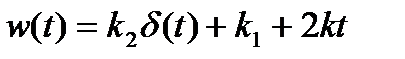 . (2.220) . (2.220)
|

Рис. 2.21. Характеристики изодромного звена 2-го порядка
В изодромных звеньях имеется некоторый начальный скачоквыходной величины, затем она неограниченно нарастает. Передаточныйкоэффициент kизодромного звена первого порядка определяет скоростьпоследующего нарастания выходной величины, второго порядка –постоянное ускорение, с которым нарастает выходная величина.
Структурные схемы.
Структурной схемойв теории автоматического управления называют графическое изображение математической модели автоматической системы управления в виде соединений звеньев. Звено на структурной схеме условно обозначают в виде прямоугольника с указанием входных и выходных величин, а также передаточной функции внутри него. Иногда вместо передаточной функции указывают уравнение или характеристику. Звенья могут быть пронумерованы и их передаточные функции, уравнения или характеристики представлены вне структурной схемы.
Основные правила преобразования структурных схем:
1. Последовательное соединение динамических звеньев.
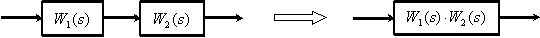
2. Параллельное соединение динамических звеньев.

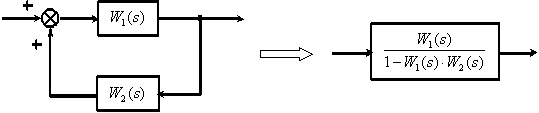
3. Замкнутый контур с отрицательной обратной связью.

4. Замкнутый контур с положительной обратной связью.
5. Перенос точки ветвления через динамическое звено.
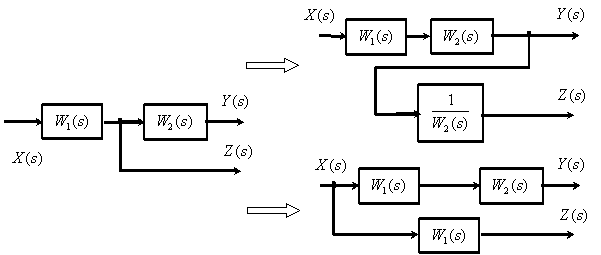
6. Перестановка суммирующих звеньев.

7. Перенос суммирующего звена через динамическое звено.

8. Перенос точки ветвления с выхода на вход суммирующего звена.

9. Перенос точки ветвления с входа на выход суммирующего звена.

10. Преобразование сумматора на три входа
X1(s)
X2(s)
Y(s)
X1(s)
X1(s)
X2(s)
X3(s)
Y(s)
X2(s)
Y(s)
X3(s)
X3(s)
Понятие устойчивости.
 В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.
В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.
Вводят понятие устойчивости «в малом», «в большом»,«в целом».Система устойчива «в малом», если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Систему называют устойчивой «в большом», когда определены границы области устойчивости, т. е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют устойчивой «в целом». Устойчивость «вцелом» для определенного класса нелинейностей называют «абсолютной» устойчивостью.
Так, например, случай, изображенный на рис. 3.1а,соответствует устойчивости «в целом», а случай, изображенный нарис. 3.1г, может соответствовать либо устойчивости «в большом», либо устойчивости «в малом». Очевидно, что система, устойчивая «в целом», будет устойчива «в большом» и «в малом»; система, устойчивая «в большом», будет устойчива и «в малом».На рис. 3.1 дизображено еще одно принципиально возможное для нелинейных систем состояние равновесия, которое называют полу устойчивым.
Дата добавления: 2018-04-05; просмотров: 1120; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
