Логарифмические частотные характеристики

Прологарифмируем выражение частотной передаточной функции

(2.98)

и получим

lnW(jω) = lnA(ω) + jφ(ω). (2.99)

Вещественной частью этого выражения является логарифм модуля, а мнимой — фаза.

Для расчетов удобно пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику(л.а.х.) и логарифмическую фазовую частотнуюхарактеристику(л.ф.х.). Для построения л.а.х находится величина:

L(ω) = 20lg|W(jω)| = 20lgA(ω) (2.100)

Эта величина выражается в децибелах.Бел представляет собой логарифми- ческую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела — в 100 раз, 3 бела — в 1000 раз и т. д.

1. Пусть модуль частотной передаточной функции равен постоянному числу ;

Toгда . (2.101)

Л. а. х. представляет собой прямую, параллельную оси абсцисс (прямая 1 на рис).

2. Рассмотрим случай, когда . Тогда (2.102)

Нетрудно видеть, что это — прямая линия, проходящая через точку с координатами и и имеющая отрицательныйнаклон 20 дб/дек,так как каждое удесятерение частоты вызовет увеличение lgω на одну единицу, т. е. уменьшение L(ω) на 20 дб(прямая 2 на рис. 2.6). Точку пересечении прямой с осью нуля децибел (осью частот) можно найти, положив L(ω) = 0 или, соответственно, А(ω) = 1. Отсюда получаем так называемую частоту среза л. а. х., равную в данном случае .

3. Аналогичным образом можно показать, что в случае л. а. х. представляет собой прямую с отрицательным наклоном 40 дб/дек (прямая 3на рис. 2.6).

4. Рассмотрим случай, когда . Тогда

. (2.103)

Нетрудно видеть, что это — прямая линия, проходящая через точку и и имеющая положительный наклон 20 дб/дек. Эта прямая может быть построена также по частоте среза ω_ср = 1/ k₃, полученной приравниванием А(ω) = 1 (прямая 4 на рис. 2.6).

Реакция системы на гармоническое воздействие.

(2.48)

Найдем математическое описание вынужденного движения системы при подаче на ее вход гармонического воздействия, например

(2.104)

Для этого решим уравнение (2.48), подставив в правую часть выражение (2.104). Общее решение имеет вид

, (2.105)

гдеу_с— общее решение однородного уравнения, а — частное решение неоднородного уравнения.

Составляющая у_с (t)определяет свободные движения (переходный процесс). В устойчивых системах она со временем затухает: у_с(t) →0при t→ ∞. Вынужденное движение описывается частным решением у_B(t).Чтобы найти его, представим входное воздействие (2.104) с помощью формулы Эйлера в виде суммы:

(2.106)

где (2.107)

Используя принцип суперпозиции, решение уравнения (2.48) можно также представить в виде суммы у = y₁+ у₂,где у₁ — решение при u = u₁в у₂— решение при u = u₂. Найдем отдельно каждое из этих решений. Подставим выражение для u₁в правую часть уравнения (2.48) вместо u. Так как

,… (2.108)

уравнение (2.48) примет вид

(2.109)

Частное решение последнего уравнения будем искать в виде

, (2.110)

где А₁ не зависит от времени. При подстановке этого выражения в (2.109) получим

(2.111)

откуда

(2.112)

Очевидно, это выражение совпадает с частотной передаточной функцией (2.92) рассматриваемой системы:

(2.113)

Подставив это выражение в формулу (2.110), получим

(2.114)

Теперь найдем частное решение исходного уравнения, подставив вместо uвыражение для из (2.107). Так как

(2.115)

(2.116)

то (2.48) в этом случае

(2.117)

Частное решение этого уравнения будем искать в виде

(2.118)

Проделав те же выкладки, что и при нахождении частного решения y₁получим

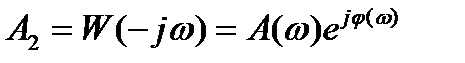(2.119)

(2.120)

Сложив (2.114) и (2.119) для у₁и у₂,найдем математическое описание вынужденного движения:

(2.121)

Таким образом, при гармоническом воздействии в устойчивых системахпосле окончания переходного процесса, выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. При этом отношение амплитуд выходной и входной величин равно модулю, а сдвиг фазы — аргументу частотной передаточной функции. Следовательно, амплитудная частотная характеристика показывает изменение отношения амплитуд, а фазовая частотная характеристика—сдвиг фазы выходной величины относительно входной в зависимости от частоты входного гармонического воздействия.

Временные характеристики.

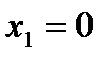Переходная функция (кривая разгона) или переходная характеристика h(t) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 2.7). Такое входное воздействие называется единичной ступенчатой функцией и обозначается , что соответствует при t ≤ 0 и при t ≥ 0. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена. Если входное воздействие представляет собой неединичную ступенчатую функцию , выходная величина будет равна .

Более строго переходную функцию можно определить как отношение выходной величины звена к высоте ступенчатого скачка на его входе, т. е. .

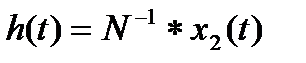Умножение какой-либо функции времени х(t) на единичную ступенчатую функцию 1(t) означает, что функция времени х(t) будет существовать только при t ≥ 0, при t < 0 она обращается в нуль(рис. 2.8).

Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 2.9). Единичная импульсная функция, или дельта-функция, представляет собой производную от единичной ступенчатой функции: . Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности.

…

Дата добавления: 2018-04-05; просмотров: 410; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!