Условия устойчивости линейных САУ

Исходное дифф. ур-ние:

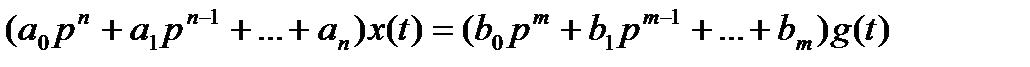(3.22)

 

р = s

(3.28)

 

Полученное алгебраическое уравнение (3.28) называют характеристическим уравнением. Его корни s₁, s₂, ....s_nбудут определять характер переходного процесса в системе.

характеристичес­кое уравнение получают обычно, приравнивая к нулю диф­ференциальный оператор привыходной величине в исходном дифференциальном уравнении(3.22), т. е.

(3.29)

 

Решение характеристи­ческого уравнения степени nсодержит nкорней. Кор­ни характеристического уравнения обыкновенного линейного дифференциаль­ного уравнения с постоян­ными коэффициентами могут быть вещественными, комплекс­ными попарно сопряженными, мнимыми попарно сопряжен­ными, нулевыми. В общем случае

(3.30)

На рис. 3.3 показаны возможные положения корней в ком­плексной плоскости корней s:

; ; ; ; ;

;       .                       (3.31)

Рис.3.3. Возможные положения корней в ком­плексной плоскости корней s.

 

Устойчивость линейной системы не зависит от вида правой части дифференциального уравнения (3.22) и определяется только характеристическим уравнением

 

 

Если все корни разные, то их называют простыми. Если среди корней есть одинаковые, то их называют кратными.

Обычно корни с отрицательными вещественными частями принято называть левыми,поскольку они в комплексной пло­скости корней расположены слева от мнимой оси, а корни с положительными вещественными частями — правыми корнями.

 

Условие устойчивости линейной системы формулируется следующим образом:

· Для того чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения (3.29)были левыми.

· Если хотя бы один корень окажется справа от мнимой оси, то система будет неустойчивой.

· Система будет находиться на границе устойчивости при наличии:

1. Нулевого корня;

2. Пары чисто мнимых корней;

3. Бесконечного корня.

Во всех трех случаях предполагается, что все остальные корни имеют отрицательные вещественные части.

 

Алгебраические критерии устойчивости.

Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристичес­кого уравнения.

. (3.37)

Из алгебраических критериев устойчивости наиболее ши­рокое распространение получили критерии устойчивости Ра­уса и Гурвица. Прежде чем познакомиться с ними, заметим, что необходи­мым условиемустойчивостисистемы любого порядка является положительность всех коэффициентов характеристического уравнения (3.37):

a₀> 0; a₁> 0; … a_n> 0 . (3.38)

Действительно, в соответствии с теоремой Безу уравнение (3.37) можно представить в виде произведения множителей, содержащих корни s_l,s₂ ,…s_n: .     (3.39)

Если все корни характеристического уравнения будут от­рицательны, то все множители выражения (3.39) будут иметь вид   ,(3.40) где  — значения корней.

Производя перемножение в (3.40), получим (3.37), в кото­ром все коэффициенты будут определяться положительными членами |а_i| выражения (3.40), т. е. будут положительны.

Если характеристическое уравнение (3.37) имеет комплекс­ные корни с отрицательными вещественными частями, то оно может быть представлено в виде

(3.41)

или

(3.42)

Уравнение (3.42) также приводится к виду уравнения (3.37) с положительными коэффициентами. Для систем первого и второго порядков необходимое условие устойчивости является и достаточным условием устойчиво­сти, поскольку в этом случае при положительных коэффи­циентах характеристического уравнения все его корни явля­ются левыми. Однако для систем третьего и высших порядков положительность коэффициентов характеристического урав­нения является необходимым условием устойчивости, но не достаточным. В этом случае все вещественные корни характе­ристического уравнения (если они есть) левые, комплексные же корни могут быть и правыми.Критерии устойчивости Рауса и Гурвица позволяют по коэффициентам характеристического уравнения (3.37) без вы­числения его корней сделать вывод об устойчивости системы.

 

 

 

Принцип аргумента

Пусть дан некоторый полином n-й степени

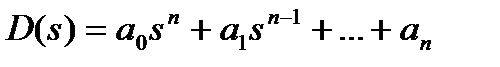                            (3.79)

Этот полином в соответствии с теоремой Безу можно представить в виде                                                                                                             ,                                                          (3.80)

где — корни уравнения D(s) = 0.

            Рис. 3.6. Геометрическое изображение корней векторами.

 

На комплексной плоскости s каждый корень геометрически может быть изображен вектором, проведенным из начала ко­ординат к точке S;      (рис. 3.6 а). Длина этого вектора равна модулю комплексного числа ,    т. е. , а угол, образованный вектором с положительным направлением действитель­ной оси, — аргументу или фазе комплексного числа ,          т. е. .

Величины геометрически изображаются векторами, проведенными из точки к произвольной точке s (рис. 3.6 б). В частном случае при s = jω получим

.                   (3.81)

Концы элементарных векторов  будут находиться на мнимой оси в точке s = jω (рис. 3.6 в).

В выражении (3.81) D(jω) представляет собой вектор, равный произведению элементарных векторов  и дей­ствительного числа . Модуль этого вектора равен произведению модулей эле­ментарных векторов и  :

                       (3.82)

а аргумент или фаза его равна сумме аргументов элементарных векторов:

.               (3.83)

Условимся считать вращение против часовой стрелки по­ложительным. Тогда при изменении ω от — ∞ до ∞ каждый элементарный вектор повернется на угол л, если его начало, т. е. корень расположено слева от мнимой оси, и на угол — π, если корень расположен справа от мнимой оси (рис. 3.7).

Рис. 3.7. Вращение векторов.

 

Предположим, что полином D(s) имеет m правых корней и n — m левых

Тогда при изменении ω от — ∞ до ∞ изменение (прираще­ние) аргумента вектора D(jω), равное сумме углов поворота векторов  равно

                                |ω = ∞

             Δ Arg D(jω)        = π(n-m)- π m= π (n-2m)                        (3.84)

                                |ω = - ∞

Отсюда вытекает следующее правило: изменение (прираще­ние) аргумента D(jω) при изменении частоты ω от — ∞ до ∞ равно разности между числом левых и правых корней урав­нения D(s) =0, умноженной на π.

Очевидно, что при изменении частоты ω от 0 до ∞ измене­ние аргумента вектора D(jω) будет вдвое меньше:

                                               |ω = ∞

                          ΔArg D(jω)        = (π/2)(n-2m)                           (3.85)

|ω = 0

Каждый из векторов , соответствующих вещественным кор­ням, повернется теперь на угол π /2 или — π /2.

Векторы ,  которые состав­ляют пару, соответствующую, например, двум комплексно-сопряжен­ным корням, повернутся: один — на угол π /2 + γ, а другой — на π /2 — γ, где γ — угол, образованный вектором, проведенным от кор­ня в начало координат, с осью абсцисс (рис. 3.8). Общее приращение аргумента произведения этих векторов при изменении ω от 0 до ∞ равно

                                  (3.86)

                               Рис.3.8. Произведение векторов

 

В основу всех частотных критериев устойчивости положе­но уравнение (3.84), определяющее приращение аргумента D(jω) при изменении ω от — ∞ до ∞, или (5) — при, из­менении ω от 0 до ∞.

 

 

---

Дата добавления: 2018-04-05; просмотров: 614; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!