Несобственные интегралы с бесконечными пределами интегрирования
Пусть функция y = f (x) определена и интегрируема на полуинтервале [a, + ∞), т.е. на любом отрезке [a, t], где t ≥ a.
Определение. Несобственным интегралом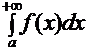 
от функции f (x) на полуинтервале [a, + ∞) называется предел:
|
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
ПРИМЕР:
Аналогично определяется несобственный интеграл на полуинтервале (−∞, b)
ПРИМЕР:
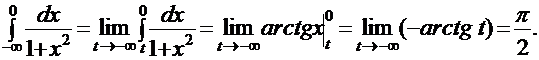
Если функция f (x) определена на всей числовой оси и для числа а сходятся несобственные интегралы 
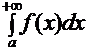и , то несобственный интеграл 
называется сходящимся. Если же хотя бы один из интегралов правой части последнего равенства расходится, то исходный интеграл с бесконечными пределами интегрирования называется расходящимся.
ПРИМЕР:
Несобственные интегралы от неограниченных функций
Пусть функция y = f (x) непрерывна, но не ограничена, на полуинтервале [a, b), т.е. точка х = а является для нее точкой разрыва второго рода. Тогда можно дать следующее определение.
Определение. Несобственным интегралом 
от неограниченной на полуинтервале [a, b) функции f (x) называется предел:
|
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.
ПРИМЕР:
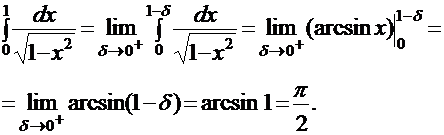
Аналогично определяется несобственный интеграл от непрерывной, но неограниченной, на полуинтервале (a, b] функции f (x):
|
|
|
|
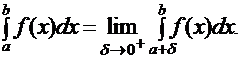
ПРИМЕР:
Рекомендуемая литература по теме 5: [1 ÷ 3].
ТЕСТ для самопроверки знаний по теме 5
1. Производная от неопределенного интеграла по переменной интегрирования равна:
· подынтегральному выражению 
· подынтегральной функции
· дифференциалу подынтегральной функции
2. Неопределенный интеграл от дифференциала некоторой функции равен:
· сумме этой функции и произвольной постоянной
· сумме производной этой функции и произвольной постоянной
· произведению этой функции и произвольной постоянной
3. Неопределенный интеграл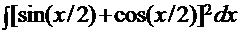 
равен:
· 
· 
· 
|
|
|
4. Неопределенный интеграл 
равен:
· 
· 
· 
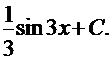
5. Формулу Ньютона-Лейбница для вычисления определенных интегралов принято записывать в виде:
· 
· 
· 
6. Определенный интеграл 
равен:
· 0.
· 1.
· 2.
7. Площадь криволинейной трапеции, ограниченной графиками функций: f (x) = 0 и g (x) = - x2, заданных на отрезке [0, 1], равна:
· 1.
· 1/3.
· 3.
|
|
|
8. Несобственный интеграл 
:
· расходится
· сходится и равен (− 1)
· сходится и равен 1
9. Несобственный интеграл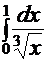 
:
· сходится и равен 3/2
· расходится
· сходится и равен 1
Тема 6. Функции нескольких переменных
Основные понятия и определения
Пусть Х – некоторое счетное множество точек (х1, х2, …, xn) пространства Rn.
Функцией нескольких переменных (n переменных) называется соответствие (закон) f, согласно которому каждой точке множества Х сопоставляется определенное число z. Такое соответствие записывается в виде z = f (x1, x2, …, xn). При этом множество Х называется областью определения функции f.
Для наглядности и простоты изложения в рамках этой темы мы ограничимся рассмотрением функций двух переменных (n = 2), хотя все основные понятия достаточно легко обобщаются на случай любого конечного числа переменных.
|
|
|
Функцию двух переменных z = f (x, y) можно изобразить графически, вычисляя для каждой точки (x, y) области ее определения Х значение функции z. В этом случае мы получим некоторую совокупность точек трехмерного пространства (x, y, z), которая и будет являться графиком функции. В самом общем случае график функции двух переменных представляет собой некоторую поверхность в трехмерном пространстве. Например, на рис. 19 приведен график функции двух переменных z = x2 + y2.
Рис. 19.
ПРИМЕРЫ:
1. Многомерная функция полезности z = f (x1, x2, …, xn) есть числовая оценка определенным индивидом полезности набора приобретенных им n товаров.
2. Производственная функция Кобба-Дугласа: 
, где А, α и β – неотрицательные константы, х1 – объем производственных фондов, х2 – объем трудовых ресурсов, z – объем выпуска продукции.
График функции двух переменных представляет собой значительно более сложный объект, чем график функции одной переменной. Чаще всего, графическое представление на плоскости достаточно сложной поверхности – графика функции встречает серьезные трудности, а самое главное, не обладает достаточной информативностью. Поэтому для изучения свойств функций двух переменных вместо графика используют так называемые линии уровня.
Линией уровня функции двух переменных z = f (x, y) называется множество точек плоскости Oxy таких, что во всех этих точках значение функции равно постоянной величине С, Число С в этом случае называется уровнем.
Фактически линии уровня представляют собой «срезы» (сечения) поверхности графика функции плоскостями с уравнениями f (x, y) = C, параллельными плоскости Oxy. Для примера на рис. 20 приведены линии уровня для некоторой функции двух переменных.
Рис. 20.
Предел и непрерывность
Для дальнейшего нам понадобится понятие δ – окрестности точки на плоскости Oxy.
Для любого числа δ > 0 δ – окрестностью точки (x0, y0) называется множество всех точек плоскости (x, y), для которых выполняются неравенства 
и 
.
Число А называется пределом функции z = f (x, y) при x→x0 и y→y0 (или в точке M0(x0, y0)), если для любого числа ε > 0 найдется число δ > 0 такое, что для всех точек M(x, y), лежащих в δ – окрестности точки М0, выполняется неравенство 
. Обозначается этот предел: 
.
Функция z = f (x, y) называется непрерывной в точке (x0, y0), если предел функции в этой точке равен значению функции в этой же точке, т.е.:
ПРИМЕР: Линейная функция 
является непрерывной в любой точке (x0, y0).
Дата добавления: 2018-04-04; просмотров: 1362; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!