Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вытекают следующие его основные свойства.
1). Производная неопределенного интеграла равна подынтегральной функции, а дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.:

2). Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.:

3). Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. если k = const ¹ 0, то:

4). Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме неопределенных интегралов от этих функций, т.е.:

Таблица основных неопределенных интегралов
В приведенной ниже таблице основных неопределенных интегралов часть формул (1÷10) следует из определения интегрирования как операции, обратной дифференцированию, и из таблицы производных простейших элементарных функций. Справедливость остальных формул легко может быть проверена дифференцированием.
1).  2).
2). 
3).  4).
4). 
5).  6).
6). 
7). 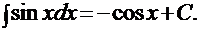 8).
8). 
9).  10).
10). 
11). 
12). 
13). 
14). 
Неопределенные интегралы, содержащиеся в этой таблице, условно называются табличными.
Основные методы интегрирования
Метод непосредственного интегрирования
Метод вычисления неопределенных интегралов сличением с табличными интегралами, с использованием основных свойств неопределенных интегралов, а также тождественных преобразований подынтегральных функций называется методом непосредственного интегрирования.
ПРИМЕРЫ:
1. Найти интеграл: 
Решение. Предложенный интеграл табличный (формула 14 таблицы при а = 4), поэтому можно записать:

2. Найти интеграл: 
Решение. Попытка сличения показывает, что данный интеграл табличным не является. Однако, принимая во внимание, что:

и используя табличные интегралы 9 и 10, получим:

Метод замены переменной
Во многих случаях удачное введение новой переменной интегрирования позволяет свести операцию нахождения интеграла к непосредственному интегрированию. Такой метод называется методом замены переменной или методом подстановки.
В основе метода замены переменной лежит формула:

|
В этой формуле  и есть замена переменной. В результате вычисления интеграла в правой части формулы получится функция, зависящая от аргумента t, поэтому, чтобы вернуться к первоначальной переменной х, нужно в полученном результате провести обратную замену
и есть замена переменной. В результате вычисления интеграла в правой части формулы получится функция, зависящая от аргумента t, поэтому, чтобы вернуться к первоначальной переменной х, нужно в полученном результате провести обратную замену 
ПРИМЕРЫ:


Рациональной тригонометрической функцией от переменных sin x и cos x называется выражение, в котором над этими переменными производятся арифметические действия (сложение, вычитание, умножение и деление).
ПРИМЕР: Выражение  является рациональной тригонометрической функцией.
является рациональной тригонометрической функцией.
Интегрирование рациональных тригонометрических функций сводится к интегрированию рациональных дробей с помощью универсальной тригонометрической подстановки:
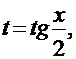
|
при этом 
ПРИМЕР:

Дата добавления: 2018-04-04; просмотров: 311; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
