Возрастание и убывание функции

⇐ ПредыдущаяСтр 7 из 20Следующая ⇒

Напомним, что функция f (x) называется возрастающей (убывающей) на промежутке Х, если для любых двух точек верно неравенство .

Сформулируем достаточный признак возрастания и убывания функции на промежутке:

Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка, то функция возрастает (убывает) на этом промежутке.

Экстремумы функции и их отыскание

Определение.Точка х₀ называется точкой локального максимума (минимума) функции f (x), если для всех х из некоторой окрестности точки х₀ выполняется неравенство f (x) ≤ f (x₀) (f (x) ≥ f (x₀)).

Локальный минимум и локальный максимум принято объединять общим названием локальный экстремум. Экстремум носит локальный (местный) характер в том смысле, что неравенства определения не должны выполняться на всей области определения функции, а должны выполняться в некоторой (небольшой) окрестности точки х₀, т.е. в некоторой локальной области. На всей же области определения функция может иметь несколько локальных экстремумов, причем может оказаться, что иной локальный максимум меньше по величине какого-то локального минимума (рис. 7):

Рис. 7.

Отыскание точек локального экстремума является важной задачей функционального анализа. Алгоритм этого отыскания базируется на ряде признаков, которые сформулированы ниже.

Необходимый признак локального экстремума

Если функция f (x) имеет в точке х₀ локальный экстремум и дифференцируема в этой точке, то

Все точки х₀, в которых производная функции обращается в нуль называются стационарными точками или точками возможного экстремума.

Необходимость приведенного признака вытекает из существования функций, для которых при выполнении условия 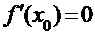экстремум в точке х₀ отсутствует. Например, таким свойством обладает функция y = x³ в стационарной точке х₀ = 0 (убедитесь в этом самостоятельно).

Достаточный признак локального экстремума

Если при переходе (в направлении слева направо) через стационарную точку х₀ производная функции меняет знак с плюса на минус, то точка х₀ является точкой локального максимума, если же – с минуса на плюс, то точка х₀ является точкой локального минимума. Если при таком переходе знак производной не меняется, то в этой стационарной точке х₀ экстремума нет.

Достаточный признак локального экстремума № 2

Дата добавления: 2018-04-04; просмотров: 291; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!