Частные производные и дифференцируемость

Функции двух переменных

Пусть z = f (x, y) – функция двух переменных. Если зафиксировать один из аргументов этой функции, например, положить y = y₀, то получим функцию одной переменной z = f (x, y₀).

Частной производной функции z = f (x, y) в точке (x₀, y₀) по переменой х называется обыкновенная производная функции z = f (x, y₀), вычисленная в точке х₀. Такая частная производная обозначается:

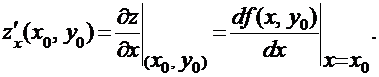
Совершенно аналогично определяется частная производная по y:

ПРИМЕР: Для функции можно записать:

Полным приращением функции z = f (x, y) в точке (x₀, y₀) называется величина:

Функция z = f (x, y) называется дифференцируемой в точке (x₀, y₀), если ее полное приращение в некоторой окрестности этой точки может быть представлено в виде:

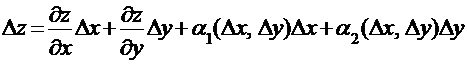где для функций α₁ и α₂ выполняются соотношения:

и .

Дифференциалом функции z = f (x, y) называется выражение:

Очевидно, что, как и в случае функции одной переменной, дифференциал функции двух переменных будет приближенно равен полному приращению функции.

Достаточное условие дифференцируемости функции двух переменных

Для того чтобы функция z = f (x, y) непрерывная в точке М₀ была дифференцируемой в этой точке, достаточно, чтобы эта функция имела конечные частные производные в этой точке и эти частные производные были бы непрерывны в точке М₀.

ПРИМЕР: Для функции частные производные существуют во всех точках и соответственно равны: Поскольку они непрерывны во всех точках, то данная функция будет дифференцируемой во всех этих точках.

Градиентом функции двух переменныхz = f (x, y) называется вектор с координатами , т.е.:

Вектор градиента в данной точке показывает направление максимальной скорости возрастания функциив этой точке. Вторым важным свойством вектора градиента является следующее: вектор градиента в данной точке перпендикулярен касательной к линии уровня, проведенной через эту точку (рис. 21):

Рис. 21.

ПРИМЕР:Найдите координаты вектора градиента функции в точке М (2, 2).

Найдем значения частных производных заданной функции в заданной точке:

Таким образом, можно записать:

Частные производные и полные дифференциалы

Второго порядка

Пусть имеется функция двух переменных z = f (x, y), которая в каждой точке своей области определения Х имеет частные производные и . Эти производные (назовем их производными первого порядка), в свою очередь можно рассматривать как некоторые функции двух переменных и .

Частными производными второго порядка функции z = f (x, y) называются частные производные от частных производных первого порядка этой функции. Они могут иметь вид:

Первые две из них принято называть повторными или просто вторыми частными производными функции z = f (x, y), а две других называются смешанными частными производными.

Если функция z = f (x, y) непрерывна на множестве Х и имеет на этом множестве непрерывные смешанные производные, то значения смешанных производных не зависят от порядка их вычисления, т.е.

Дифференциалом второго порядка функции z = f (x, y) называется величина:

Заметим, что по своей структуре дифференциал второго порядка функции двух переменных представляет собой квадратичную форму относительно дифференциалов аргументов, т.е. может быть записан в виде:

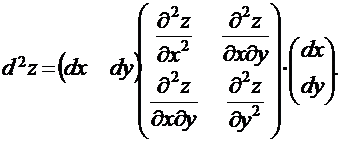
Дата добавления: 2018-04-04; просмотров: 549; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 15 161718 19 20 Следующая ⇒

Мы поможем в написании ваших работ!