Достаточный признак сходимости знакопеременного ряда

Если ряд, составленный из модулей членов знакопеременного ряда, сходится, то сходится и исходный знакопеременный ряд.

Ряд называется абсолютно сходящимся, если сходится сам ряд, так и ряд, составленный из модулей его членов.

Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из модулей его членов, расходится.

ПРИМЕР: Ряд является условно сходящимся, поскольку сам этот ряд сходится по признаку Лейбница (убедитесь в этом сами), а ряд, составленный из модулей его членов , расходится как гармонический ряд.

Степенные ряды

Степенным рядом называется ряд, имеющий вид:

Где a_n – действительные числа, а число y₀ называется центром степенного ряда.

Замена x = y – y₀ переводит степенной ряд к новому виду, который называется степенным рядом с нулевым центром:

ПРИМЕР: Ряд 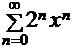является степенным рядом с нулевым центром.

Совокупность значений х, при которых степенной ряд с нулевым центром сходится, называется областью сходимости степенного ряда.

Структура области сходимости степенного ряда устанавливается следующей теоремой.

Теорема Абеля

Если степенной ряд сходится при x = x₀ ¹ 0, то он сходится и притом абсолютно, при всех х таких, что ½х½< ½x₀½. Если степенной ряд расходится при х = х₁, то он расходится при всех х таких, что ½х½> ½x₁½.

Радиусом сходимости степенного ряда с нулевым центром называется число R ³ 0 такое, что при ½х½< R ряд сходится, а при ½х½> R ряд расходится. При этом интервал (- R, R) называется интервалом сходимости степенного ряда.

Замечание.На концах интервала сходимости, т.е. при х = ± R, ряд может как сходиться так и расходиться.

Радиус сходимости степенного ряда определяется формулой:

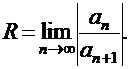
ПРИМЕРЫ:

1. Для степенного ряда 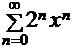найдем: . Поэтому данный ряд сходится на интервале

2. Для степенного ряда 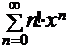найдем: . Поэтому данный ряд сходится только в одной точке х = 0.

Специфическими разновидностями конечных степенных рядов являются ряды Тейлора и Маклорена.

Пусть функция f (x) имеет в точке а и в некоторой ее окрестности производные порядка до (n + 1) включительно, а х – любое значение аргумента из указанной окрестности и х ¹ а. Тогда существует точка q Î (а, х) такая, что справедлива формула:

Эта формула называется формулой Тейлора, а представление функции в виде степенного ряда называется разложением функции в ряд Тейлора. Последнее слагаемое в формуле Тейлора

называется остаточным членом и характеризует абсолютную погрешность представления функции в виде ряда Тейлора с n слагаемыми.

Если в формуле Тейлора положить а = 0, то получим формулу Маклорена:

Представление функции в виде степенного ряда по формуле Маклорена называется разложением функции в ряд Маклорена.

Обе приведенные формулы позволяют с контролируемой точностью заменять любые дифференцируемые функции многочленами (конечными степенными рядами) в некоторой, небольшой, окрестности либо точки а (ряд Тейлора), либо точки 0 (ряд Маклорена).

ПРИМЕР: Разложить функцию в ряд Маклорена.

Поскольку все производные нечетного порядка заданной функции имеют вид и, следовательно, при х = 0 равны (- 1), а все производные четного порядка при х = 0 равны 1, можно заданную функцию представить в виде:

Рекомендуемая литература по теме 7:[1 ÷ 3].

ВОПРОСЫ для самопроверки знаний по теме 7:

1. Что можно сказать о сходимости числового ряда с положительными членами , если известно, что ряд сходится?

2. Будет ли сходящимся ряд с положительными членами, для которого предел отношения последующего члена к предыдущему члену равен 2?

____________________________________________________________

3. Будет ли сходящимся знакопеременный ряд, если ряд, составленный из модулей его членов, сходится?

4. Выполнения каких условий достаточно для сходимости знакочередующегося ряда?

5. Как называется множество всех значений х, при которых степенной ряд с нулевым центром сходится?

6. Обязательно ли сходится степенной ряд при x = ± R, где R – радиус его сходимости?

7. Какую функцию можно представить в виде разложения в ряд Тейлора?

ЛИТЕРАТУРА

1. Налимов В.Н. Основы математического анализа для экономистов: Учебное пособие. – М.: Издание ИМЭС, 2013.

2. Налимов В.Н. Основы высшей математики для экономистов. Лекционный курс: Учебное пособие по курсу «Математика». – М.: Издание ИМЭС, 2006.

3. Налимов В.Н. Основы высшей математики для экономистов. Практические занятия (семинары): Учебное пособие по курсу «Математика». – М.: «Весть», 2007.

Дата добавления: 2018-04-04; просмотров: 471; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 15 16 17 18 1920

Мы поможем в написании ваших работ!