Расчет изменения энергии Гиббса при протекании химической реакции с применением таблиц стандартных термодинамических величин

Зависимость энергии Гиббса от давления и температуры, уравнение Гельмгольца-Гиббса.
Зависимость энергии Гиббса от температуры и давленияΔH – TΔS = U + pV– TΔS = G(7.21)
DH характеризует общее изменение энергии системы в ходе процесса, а изменение энергии Гиббса показывает, какая часть ее может быть превращена в полезную работу, поэтому раньше ее называли свободной энергией, в противоположность энтропийному члену, который характеризовал связанную энергию, недоступную для превращения в работу. а)  ; б)
; б)  (7.20) Из уравнения 7.20а следует, что с ростом давления энергия Гиббса увеличивается, так как V> 0, но темп роста замедляется, так как объем постепенно уменьшается. Причем для разных идеальных газов эти кривые будут одинаковыми.
(7.20) Из уравнения 7.20а следует, что с ростом давления энергия Гиббса увеличивается, так как V> 0, но темп роста замедляется, так как объем постепенно уменьшается. Причем для разных идеальных газов эти кривые будут одинаковыми.
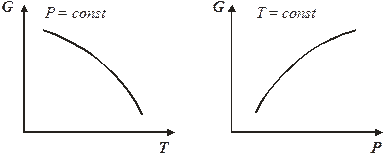
С ростом температуры энергия Гиббса убывает, так как энтропия всегда положительна, причем падение энергии Гиббса будет ускоряться из-за роста энтропии при повышении температуры.
Уравнение Гиббса - Гельмгольца.
Сочетанием уравнений 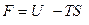 и
и 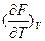 = -S и
= -S и
Гиббса  и
и 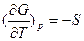
можно получить уравнения Гиббса-Гельмгольца:
 и
и 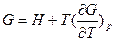
характеризующие запас свободной энергии для данного состояния системы в изотермических условиях.
На основе этих уравнений получают уравнения Гиббса-Гельмгольца для изменения термодинамических потенциалов:
 и
и  эти уравнения не используют в явном виде энтропию. Или:
эти уравнения не используют в явном виде энтропию. Или:
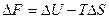 и
и 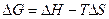
Эти уравнения наиболее применимы для расчета изменений функций Гельмгольца и Гиббса при протекании химических реакций. Они связывают максимально полезную работу, при переходе системы из состояния 1 в состояние 2 с тепловым эффектом перехода системы из состояния 1 в состояние 2.
Легко показать, что

т.е. энергия Гиббса отличается от изменения энергии Гельмгольца на величину 
т.е. на изменение числа молей газообразных продуктов в ходе реакции.
Понятие о летучести и термодинамической активности.
В 1901 г. Льюис для реальных газов ввел понятие летучести (илифугитивности) f.
Летучесть – это та величина, которую в случае реальных газов необходимо подставлять вместо давления в соответствующие соотношения, описывающие свойства идеальных газов, чтобы они же были применимыми и для описания свойств реальных газов.
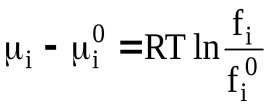 (77)
(77)
В формуле (77) fi ¹p i.
При р®0 реальный газ по свойствам приближается к идеальному газу, поэтому:
 (78)
(78)
При p ® 0, f = р, т.е. газ ведет себя как идеальный.
Мерой отклонения свойств реального газа от идеального служит коэффициент активности g (коэффициент летучести или фугитивности) 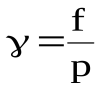 .
.
При p® 0, р ®f и g ®1
Введем понятие активности: 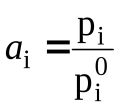 (79)
(79)
ai – активность i-го компонента в смеси идеальных газов,
ai – безразмерная величина, поскольку принимается, что рi0 = 1 атм, тогда
ai = pi (80)
т.е. для идеального газа его активность численно равна его давлению, выраженному в атмосферах.
Для реального газа: 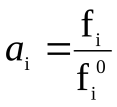 ,
,
fi0 = 1 атм, ai = fi – безразмерная величина.
С учетом сказанного выше выражение для химического потенциала любого газа (в смеси) можно записать в следующее выражение:
μi= μ0i + 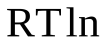 ai
ai
Тогда, для идеальных растворов
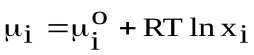 ; (81)
; (81)
xi– мольная доля i компонента в растворе.
?? Применительно к реальным растворам вместо фугитивности применяют активность.
 , (82)
, (82)
где 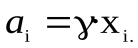 и
и  при
при  , а
, а 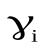 (коэффициент активности) характеризует отклонение свойств реального раствора от идеального.
(коэффициент активности) характеризует отклонение свойств реального раствора от идеального.
Дата добавления: 2018-02-28; просмотров: 961; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
