Химический потенциал и химическое равновесие

Химическое равновесие – такое состояние системы, что при некоторой температуре энтальпийный и энтропийный факторы совпадают, т.е ΔH=TΔS=0. В этом случае Δ G=0 – условие термодинамического равновесия. При термодинамическом равновесии скорость в прямом направлении равна скорости в обратном.

Химический потенциал ”μ”.Значение химического потенциала нельзя измерить, но можно рассчитать исходя из уравнения связывающего химический потенциал с составом: μ_i=μ_i^o+RTlnK, где K={P_i-парциальное давление, C_i-концентрация, Cm_i-массовая доля, X_i-мольная доля} – константа. Для реальных растворов μ_i=μ_i^o+RTlnA_i

Хими́ческийпотенциа́л μ — один из термодинамических параметров системы, а именно энергия добавления одной частицы в систему без совершения работы. Определение химического потенциала можно записать в виде:

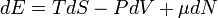
где Е — энергия системы, S — её энтропия, N — количество частиц в системе.

Эта формула определяет, кроме химического потенциала μ, также давление P и температуру T.

,

где G — потенциал Гиббса.

Если энергия системы зависит не от объёма, а от других термодинамических параметров A₁,A₂..., исходная формула принимает вид

Если в системе имеется несколько разных типов частиц, есть столько же разных химических потенциалов.

Парциальные и интегральные мольные величины и методы их определения.

Рассмотрим, какие еще термодинамические переменные и функции (кроме концентраций) необходимы для описания свойств растворов. Прежде всего к раствору как целому применимо понятие молярных термодинамических функций – внутренней энергии, энтальпии, энтропии, свободной энергии, относящихся к одному молю раствора. Под молем раствора подразумевают массовое количество М раствора, содержащее N_A (число Авогадро) молекул, в которых представлены все компоненты раствора пропорционально их мольным долям: М = Sx_i·M_i.

Молярные величины для всего раствора обозначаются заглавной буквой с нижним индексом “m”, например DH_m,S_m.

Отметим, что, поскольку компоненты раствора из-за взаимного влияния есть вещества с новыми термодинамическими свойствами, термодинамические функции раствора в общем случае не есть алгебраические суммы соответствующих функций для чистых компонентов. Поэтому для описания компонентов растворов как веществ в новом состоянии используют парциальные молярные величины – внутреннюю энергию, энтальпию, энтропию, свободную энергию и т.п., относящиеся к одному молю индивидуального вещества в растворе. Парциальные молярные величины для компонентов растворов обозначаются соответствующей заглавной буквой с чертой над ней, например _.

Парциальные величины – аналог молярных величин для чистых веществ, но характеризующие данное вещество в конкретном растворе с конкретнойконцентрацией. Т.е., они являются функциями не только пары простых термодинамических переменных, но и всех концентраций:

Исходя из физического смысла парциальных молярных величин (характеристик компонентов раствора) и молярных величин (характеристик всего раствора), легко увидеть линейную связь между ними:

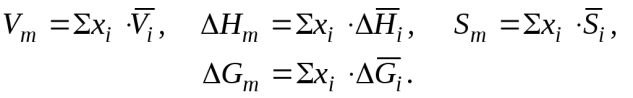(6.1)

Продифференцировав (6.1) по концентрациям, получаем следующие соотношения:

(6.2)

которые во многих работах используют в качестве первичных определений парциальных молярных величин. В силу существования соотношений (6.2), часто термодинамические величины, относящиеся к раствору, называют интегральными.

Парциальные величины (энтальпия, энтропия, свободная энергия и т.п.) зависят от набора и концентраций индивидуальных веществ, образующих раствор. Т.е. парциальные молярные величины должны являться функциями не только температуры и давления (как для чистых веществ), но и качественного и количественного состава раствора. Важно отметить, что для расчетов равновесий в системах, содержащих растворы, следует пользоваться условием равенства именно парциальных молярных потенциалов Гиббса индивидуальных веществво всех К фазах системы:

Здесь римские цифры означают номер фазы (раствора).

Например, давление насыщенного пара i-го компонента раствора определяется из уравнения:

(6.3)

Для характеристики энергетических изменений в процессе образования раствора используют такие понятия, как термодинамические функции смешения, относящиеся как к одному молю раствора(интегральные величины), так и к каждому компоненту в отдельности(парциальные величины).Характеристики процесса смешения обозначаются верхним индексом “М” – от английскогоMixing – смешение.

Парциальные молярные характеристики смешения в металлургии вводятся по определению какразница между значением функциидля одного моля компонента в раствореи соответствующим значениемдля чистого компонента:

(6.4)

По физическому смыслу это означает, что для веществ в состоянии раствора за начало отсчета термодинамических функций приняты их значения для чистых веществ:

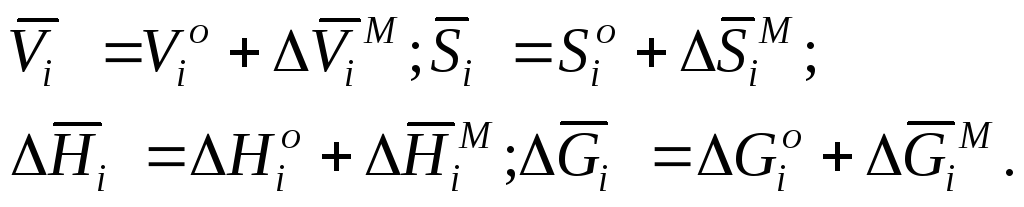(6.5)

Или, по-другому, для веществ в растворах в качестве стандартного состояния выбрано их состояние в виде чистых веществ.Данный способ определения стандартного состояния для вещества в растворе называется симметричным: все компоненты раствора равноправны. Преимуществом такого выбора стандартного состояния является физическая прозрачность его формального определения и сравнительная легкость получения стандартных величин из опыта.

Интегральные молярные характеристики процесса смешения вводятся как разница между значением функции для одного моля раствора и соответствующим значением для набора чистых компонентов, взятых в количествах, необходимых для образования раствора заданного состава:

(6.6)

Иными словами, интегральная молярная термодинамическая характеристика процесса смешения есть ее изменение при образовании одного моля раствора из чистых веществ, соответственно взятых в количествахx_iмолей каждого.

Особое значение имеет интегральная молярная Dэнтальпия HM, называемая такжетеплотой смешенияили теплотой образования одного грамм–моля раствора. Это – тепло, которое выделяется (или поглощается) при образовании в сумме одного моля раствора изх_iмолей чистых веществ и которое экспериментально легко определяется в калориметре. Измерив теплоту смешения, легко рассчитать интегральную молярную энтропиюDSM и интегральную молярную свободную Dэнергию смешения ГиббсаGM. Последняя величина есть работа, необходимая для образования одного моля раствора изх_iмолей чистых веществ (за исключением работы расширения). Если свободная энергия смешения отрицательна, то процесс образования раствора (сплава) самопроизволен; если положительна – то для получения сплава придется использовать специальные технологические приемы.

В заключение приведем сводную таблицу 6.1. соотношений между парциальными и интегральными молярными величинами (на примере энтропии).

Таблица 6.1. Основные термодинамические соотношения для растворов

молярные величины
Парциальные (для i-го компонента)	Интегральные (для раствора в целом)
Абсолютные
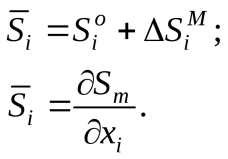
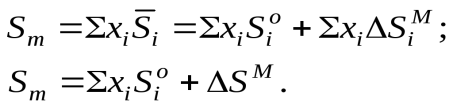
Смешения

 

Уравнение Гиббса-Дюгема.

ГИББСА-ДЮГЕМА УРАВНЕНИЕ, связывает изменения т-ры Т, давления р и хим. потенциалов компонентов равновесных термодинамич. систем. В общем виде записывается в форме:

где n_i-число молей i-того компонента. Для процессов, происходящих при постоянных Т и р, Гиббса - Дюгема уравнение устанавливает связь между изменениями хим. потенциалов компонентов и Наиб. широко используется в термодинамике р-ров. Для р-ровнеэлектролитов употребительны след. формы ур-ния:

где 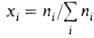-молярная доля i-того компонента, а_i-его активность, связанная с соотношением:

-хим. потенциал компонента в стандартном состоянии, R-газовая постоянная). Форма записи Гиббса - Дюгема уравнения для коэффициентов активности зависит от способа выражения концентрации (в молярных долях, молярности или моляльности). При выражении концентрации в молярных долях для р-ровнеэлектролитов и Гиббса - Дюгема уравнение имеет вид: Для р-ров электролитов разработаны спец. формы 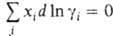записи Гиббса - Дюгема уравнения.

Гиббса - Дюгема уравнение позволяет определять зависимость от состава хим. потенциала, активности или коэф. активности одного из компонентов бинарного р-ра, если подобная зависимость известна для др. компонента (в случае многокомпонентных р-ров-для всех остальных компонентов). Гиббса - Дюгема уравнение применяют также для определения активности компонентов бинарного р-ра по данным о равновесном общем давлении пара над р-ром при данной Т.; с его помощью проверяют термодинамич. согласованность экспериментально определенных значений активности в-в.

Понятие идеального раствора.

Идеальным раствором называют раствор, для которого выполняется первый закон Рауля.

Идеальными при любых концентрациях являются растворы, компоненты которых близки по физическим и химическим свойствам (оптические изомеры, гомологи и т. п.), и образование которых не сопровождается объёмными и тепловыми эффектами. В этом случае силы межмолекулярного взаимодействия между однородными и разнородными частицами примерно одинаковы, и образование раствора обусловлено лишь энтропийным фактором.

Первый закон Рауля:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причём коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

Для бинарного раствора, состоящего из компонентов А и В (компонент А считаем растворителем) удобнее использовать другую формулировку:

Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе.

Предельно разбавленный раствор получают путем последовательного разбавления исследуемого раствора чистым растворителем.

---

Дата добавления: 2018-02-28; просмотров: 3003; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!