Диаграммы состояния однокомпонентных систем: воды, серы

⇐ ПредыдущаяСтр 15 из 40Следующая ⇒

Диаграмма состояния воды.Разберем закономерности фазовых равновесий на примере диаграммы состояния воды (рисунок 24), построенной на основе экспериментальных данных. Внешними параметрами, влияющими на равновесие, являются температура и давление. Для однокомпонентных систем максимальное количество сосуществующих стабильных равновесных фаз не может быть более трех (Ф=К+2), что возможно только при нонвариантном состоянии воды (Ф=К+2-С=1+2-0=3).

На диаграмме состояния воды линии ОА, ОВ, ОС определяют совокупность значений давлений и температуры, при которых в равновесии одновременно находятся сразу две фазы: лед - вода, вода - пар, либо лед - пар, для которых выполняется уравнение Клапейрона - Клаузиуса. Системы одновариантны (С=К-Ф+2=1-2+2=1), что указывает на возможность сохранять двухфазное равновесие только при условии произвольного изменения лишь одного параметра (или давления, или температуры), другой же параметр меняется по строго определенному закону. Линия ОА имеет наклон влево, так как 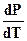<0. Однако этот наклон небольшой, потому что изменение объема при фазовом переходе лед - жидкая вода составляет не более 10%. Линии фазового перехода жидкой воды в парообразную, а также твердой в парообразную, для которых 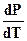>0 , имеют наклон вправо, причем значительный вследствие резкого изменения объема фазы.

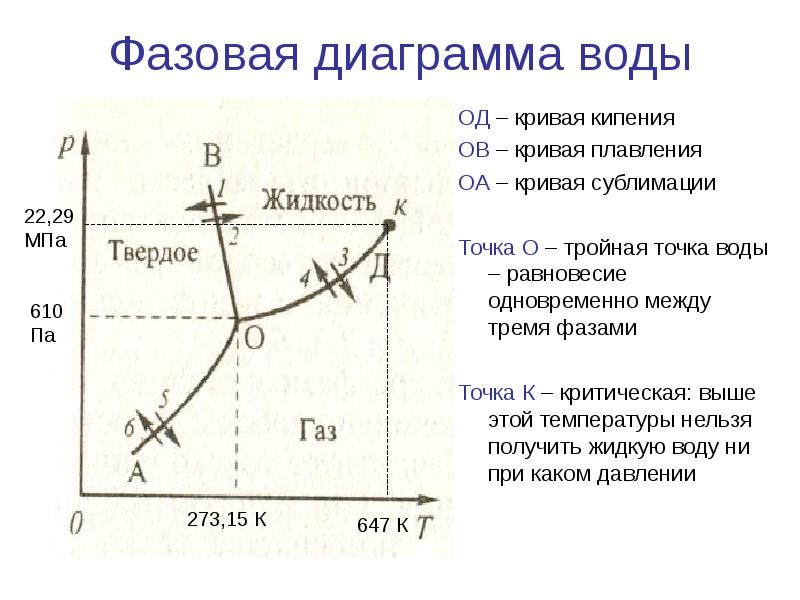
Три указанные линии сходятся в точке О, координаты которой характеризуют такое состояние воды, когда в равновесии сразу находится вода в трех агрегатных состояниях. Степень свободы такого равновесия равна нулю (С=К-Ф+2=1-3+2=0), поэтому существует это трехфазное равновесие только при строго определенных условиях (Р=6,1 гПа, Т=273,1576К). Пунктирная линия ОД (как продолжение кривой ОВ) показывает совокупность координат неустойчивого (метастабильного) состояния переохлажденной воды.

Для однофазной воды - жидкой, твердой или парообразной (например, точки 1, 2, 3, которые называются фигуративными) степень свободы равна двум (С=К-Ф+2=1-1+2=2), поэтому для сохранения двухвариантного состояния воды можно по желанию изменять сразу два параметра: и давления, и температуры (но в области, заключенной между линиями двухфазного состояния).

При больших давлениях (примерно 200 – 4000 МПа) твердый лед имеет шесть модификаций (это не отражено на рисунке 24). Таким образом, вода может иметь восемь фаз (жидкую, парообразную и шесть твердых), однако, как было указано выше, в равновесии может сосуществовать не более трех.

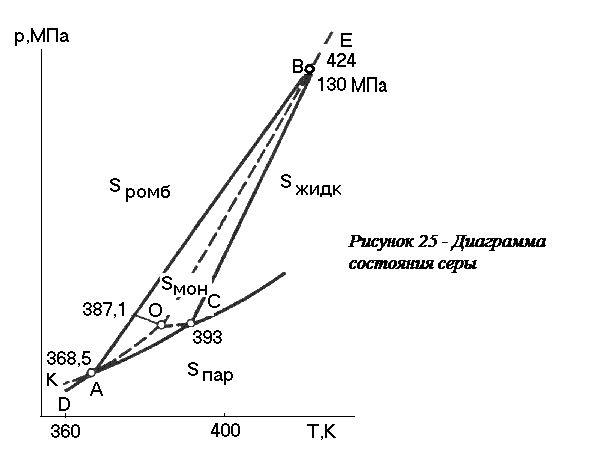
Диаграмма состояния серы.Сера может находиться в форме четырех устойчивых фаз: жидкой, газовой (парообразной), двух твердых (кристаллических): ромбической и моноклинной, условия существования которых показаны на диаграмме состояния (рисунок 25).

Для серы характерны 4 безвариантных трехфазных точки - А, В, С, О (С=К-Ф+2 = 1-3+2=0). Координаты этих точек показывают значения температуры и давления, при которых сосуществуют следующие фазы серы: в точке А- ромбическая + моноклинная + парообразная, в точке В - ромбическая + моноклинная + жидкая, в точке С - моноклинная + жидкая + парообразная, в точке О – перегретая ромбическая (кривая ОВ) + переохлажденная жидкая (кривая ОС) + пар (кривая АО). Важно отметить для точки О две особенности: а) давление пара над переохлажденной жидкостью (кривая ОС) выше давления пара, равновесного с моноклинной серой (кривая АС); б) сосуществующие фазы являются неустойчивыми и поэтому образуют метастабильную, малоустойчивую систему.

Кривая СВ являются линией плавления (кристаллизации) моноклинной серы, кривые AD и АC характеризуют сублимацию (осаждение) соответственно ромбической и моноклинной серы, ВЕ и CF показывают условия плавления (конденсации) ромбической серы и испарения (конденсации) серы, а линия АВ соответствует равновесию серы ромбической и серы моноклинной. Так как мольный объем ромбической серы меньше моноклинной, то в соответствии с уравнением Клапейрона-Клаузиуса кривая равновесия имеет наклон вправо.

Пунктирной линией показаны метастабильные (неустойчивые) равновесия моноклинной серы.

Из диаграммы состояния серы следует, что моноклинная сера существует только в области координат, заключенных кривыми АВС

38. Монотропные и энантиотропные фазовые переходы. Правило ступеней Оствальда. Энантиотропные и монотропные фазовые превращения. Многие вещества в твердом состоянии (например, вода, сера) имеют несколько кристаллических модификаций, которые существуют в виде отдельных фаз. Обратимые полиморфные фазовые переходы, когда данная кристаллическая форма твердого вещества переходит в другую при изменении внешних условий, а затем вновь восстанавливается при создании прежних условий, называются энантиотропными превращениями. Примером такого превращения может служить фазовый переход ромбической серы в моноклинную (и наоборот) (рисунок 25, линия АВ).

Полиморфное превращение, когда самопроизвольно возможен только односторонний переход одной метастабильной модификации в другую, а обратный самопроизвольный переход невозможен, называется монотропным превращением. Такой фазовый переход имеется у бензофенона (рисунок 26), когда a - модификация (температура плавления 298К) всегда метастабильна и может самопроизвольно переходить только в b - форму (температура плавления 321К), обратный самопроизвольный процесс невозможен, так как давление пара над a - кристаллами всегда выше, чем над кристаллами b- формы. А при фазовых переходах процесс подчиняется правилу ступеней Оствальда: вначале образуется менее устойчивая модификация.

В химии известно правило ступеней Оствальда, которое гласит, что в случае возможности ряда превращений от менее устойчивого состояния к все более устойчивым, обычно образуется ближайшая более устойчивая система, а не самая стабильная.

???39.Диаграммы кипения двухкомпонентных жидкостей. Закон Рауля.

Каждой жидкости при данной температуре соответствует определенное давление насыщенного пара р₀. С повышением температуры р₀ увеличивается. При растворении в жидкости какого-либо нелетучего вещества давление насыщенного пара растворителя над раствором становится ниже, чем над чистым растворителем при той же температуре. Причем понижение давления пропорционально концентрации раствора.

Относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества.

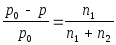= N₂, (1.4)

где

p₀- давление насыщенного пара над чистым растворителем;

p - давление насыщенного пара растворителя над раствором;

N₂ - мольная доля растворенного вещества;

n₁- число молей растворенного вещества;

n₂ - число молей растворителя.

Понижение давления насыщенного пара растворителя над раствором нелетучего вещества приводит к повышению температуры кипения и понижению температуры замерзания раствора по сравнению с чистым растворителем, что находит отражение на диаграмме состояния растворителя. На рис.1.1 приведена диаграмма состояния воды и водного раствора нелетучего вещества. Согласно закону Рауля давление водяного пара над водным раствором ниже, чем над водой. Температура кипения жидкости Т_кип - это температура, при которой давление насыщенного пара ее достигает атмосферного давления; для воды это 100^оС (при давлении 101,3 кПа или 1,013^.10⁵ Н/м²). Так как над раствором давление насыщенного пара растворителя ниже, для того чтобы раствор закипел, его надо нагреть до более высокой температуры, чем чистый растворитель. Поэтому кривая 4 кипения для раствора (см. рис 1.1.) лежит правее, чем (кривая 1) для воды. Кривая 3 соответствует изменению давления насыщенного пара над твердой водой (льдом) при переходе ее из твердого в газообразное состояние.

Правило рычага.

Фигуративнаяточка – любая точка на диаграмме, характеризующая температуру и состав системы.

Коннода (нода) – соединительная линия двух сопряженных точек (изотерма).

Изоплета– линия постоянного состава.

Количественные соотношения между массами фаз гетерогенной системы находят с помощью правила рычага.

Рассмотрим систему, изображенную на рис.3.8.

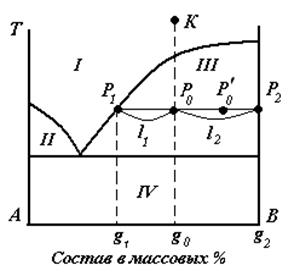
Рис.3.8. Фазовая диаграмма с эвтектикой для определения содержания компонентов по правилу рычага.

Точка К – ненасыщенный расплав состава g₀.

Точка Р₀, состава g₀, отражает валовый (общий) состав.

Точки Р₁ состава g₁ и Р₂ состава g₂ отражают состав жидкой и твердой фаз соответственно (сопряженные точки).

Р₀=Р₁+Р₂ (3.13)

Составим материальный баланс по компоненту В.

g₀ – процентное содержание компонента Вв системе;

g₁ – процентное содержание компонента Вв жидкой фазе;

g₂ – процентное содержание компонента Вв твердой фазе.

Материальный баланс компонента В можно описать уравнением:

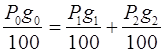, (3.14)

отсюда:

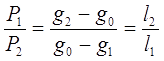(3.15)

Уравнение (3.15) называется правилом рычага.

Правило рычага: отношение масс жидкой и твердой фазы обратно пропорционально отношению отрезков, на которые делит данная фигуративная точка конноду (ноду).

Первый закон Коновалова.

Состав пара равен составу жидкости, из которой он образовался, только для идеальных растворов при условии равенства давлений насыщенного пара обоих чистых компонентов (P_A^o=P_B^o). Это наблюдается очень редко и характерно лишь для оптических изомеров. В общем случае составы пара и жидкости в состоянии равновесия различны. Если раствор состоит из двух летучих жидкостей, то пар, находящийся в равновесии с жидким раствором, будет содержать оба компонента. Зависимость состава пара от состава раствора описывается законами, установленными опытным путем Коноваловым Д.П.

Первый закон Коновалова: Пар по сравнению с равновесным раствором богаче тем компонентом, добавление которого в систему повышает общее давление пара или понижает температуру кипения смеси при данном внешнем давлении.

Этот закон может быть сформулирован также следующим образом:

Парообразная фаза по сравнению с жидкой обогащена более летучим компонентом, то есть тем компонентом, температура кипения которого ниже.

Первый закон Коновалова можно проиллюстрировать с 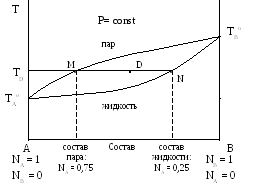помощью диаграммы кипения (рис. 7).

п ↔ ж

Рис. 7 – Зависимость температуры кипения раствора от состава пара (T_A^оMT_B^о) и от состава жидкости (T_A^оNT_B^о) приP=const.

Диаграммы кипения строятся на основе экспериментальных данных при условии постоянства давления в координатах температура кипения – состав пара и состав жидкости. По осям ординат указаны температуры кипения чистых индивидуальных веществ A и B (T_A^о и T_B^о). Линия T_A^оMT_B^о графически отражает зависимость температуры кипения растворов от состава пара. Выше этой линии на диаграмме находится область, соответствующая парообразному состоянию системы. Линия T_A^оNT_B^охарактеризует зависимость температуры кипения растворов от состава жидкости. Ниже этой линии на диаграмме находится область, соответствующая жидкому состоянию системы. Между линиями находится область, соответствующая двухфазному состоянию системы (область гетерогенности). Например, для состава, отмеченного точкой D на диаграмме, при температуре T_D в равновесии будут находиться пар, состав которого характеризуется точкой M, и жидкость, состав которой соответствует точке N на линии жидкости. Температура кипения вещества A ниже температуры кипения вещества B (T_A^o<T_B^o) , то есть жидкость A является более легкокипящей. Поэтому в соответствии с первым законом Коновалова в паре будет больше компонента A, чем в жидкости, в равновесии с которой находится этот пар. Например, для состава указанного на диаграмме точкой D жидкость содержит 0,25 мольных долей (25 % мольн.) низкокипящего компонента A, а пар, находящийся в равновесии с этой жидкостью содержит 0,75 мольных долей (75 % мольн.) данного компонента A (рис. 7).

??42.Второй закон Коновалова.

Второй закон Коновалова. При значительных отклонениях от закона Рауля на кривых, отражающих зависимость общего давления от состава бинарных растворов (при Т = const) появляются максимумы или минимумы, а на диаграммах кипения этих систем кривые, отражающие зависимость температур кипения от состава пара и от состава жидкости, имеют общие точки (С) (рис. 8 и 9).

Для таких систем Коноваловым установлен второй закон, который формулируется следующим образом: точки максимума или минимума на кривых общего давления отвечают растворам, состав которых одинаков с составом равновесного с ними пара.

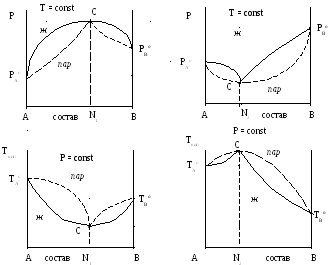
Рис. 8 – Диаграммы равновесия пар –

жидкий раствор с большим положительным отклонением от закона Рауля.

Рис. 9 – Диаграммы равновесия пар – жидкий раствор с большим отрицательным отклонением от закона Рауля.

Точкам максимума на кривых зависимости давления от состава соответствуют точки минимума на кривых температура кипения – состав. И, наоборот, точкам минимума на зависимостях давления от состава соответствуют максимумы на зависимостях температур кипения от состава. Растворы, отвечающие по составу этим экстремальным точкам называются азеотропнымиили нераздельно кипящими (точки С на рис. 8 и 9). Состав этих растворов не меняется при кипении, а температура кипения при заданном внешнем давлении остается постоянной, как у чистых веществ.

С помощью диаграмм кипения, примеры которых приведены в настоящем пособии, можно определять температуры начала и окончания кипения растворов, температуры начала и окончания конденсации пара заданного состава, составы жидкой и пароообразной фаз, находящихся в равновесии, вычислить относительное количество жидкой и парообразной равновесных фаз по правилу рычага.

Дата добавления: 2018-02-28; просмотров: 4250; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Мы поможем в написании ваших работ!