Расчет теплового эффекта химической реакции при любой температуре по табличным термодинамическим данным. (см задачи)

Второй закон термодинамики. Математическое выражение.

В изолированных системах могут самопроизвольно протекать только процессы, идущие с увеличением энтропии (ΔS>0).

Математическое выражение второго закона термодинамики записывается:

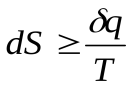
Здесь знак > относится к необратимым процессам, а знак = к обратимым. Так как энтропия является функцией состояния, ее изменение при протекании как обратимого, так и необратимого процессов одинаково. Поэтому при расчете изменения энтропии необходимо пользоваться формулами для обратимых процессов.

Энтропия обладает свойствами аддитивности, поэтому изменение энтропии в сложном процессе равно сумме изменений энтропий в отдельных его стадиях. Абсолютное значение энтропии какого-либо вещества при любой температуре можно рассчитать, если известна абсолютная энтропия при какой-то одной температуре, например, при 298К и температурные коэффициенты теплоемкости:

Изменение энтропии в различных процессах вычисляют по следующим уравнениям:

При нагревании n – моль вещества от Т₁ до Т₂ при P = const:

где

Интегрирование дает:

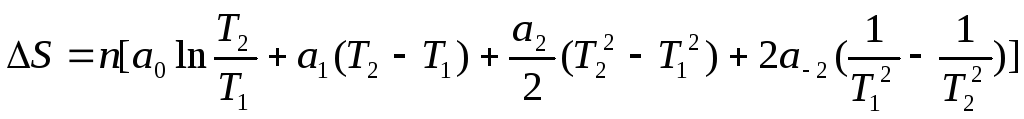
Математическое выражение для энтропии Клаузис получил из цикла Карно, на котором основана работа тепловой машины.

Рабочее тело (1 моль идеального газа ) получает от нагревателя с температурой Т₁ некоторое количество теплоты Q₁ и, расширяясь изотермически (кривая АВ), совершает работуА₁Далее газ расширяется адиабатно, без подвода тепла (кривая ВС) и его температура падает до Т₂ . Совершаемая в этом процессе работа равна А₂ .

Затем совершаются два процесса сжатия газа: изотермическое сжатие (кривая СD) при температуре Т₂ в результате которого газ отдает приемнику теплоту Q₂ и адиабатное сжатие (кривая ДА) с повышением температуры газа до Т₁ .В процессах сжатия над газом производится работа А ₃ и А ₄ соответственно. Все эти процессы обратимы.

Энтропия как функция состояния и критерий направления процесса в изолированной системе.

Энтропия – критерий направления самопроизвольного процесса в изолированной системе.

В изолированных системах отсутствует подвод теплоты из внешней среды (Q = 0), поэтому, согласно II закону термодинамики (2), в изолированной системе энтропия либо остается постоянной в состоянии равновесия, либо возрастает при необратимом (самопроизвольном) течении процесса. Рост энтропии продолжается до установления равновесного состояния, при этом значение энтропии максимально S_max (рисунок- t,s-диаграмма).

Изменение энтропии однозначно определяет направление и предел самопроизвольного протекания процесса только для изолированных систем: если в результате расчета окажется, что DS> 0, процесс пойдет самопроизвольно, при DS = 0 – состояние равновесия, если DS< 0, процесс самопроизвольно протекать не будет.

Энтропия – функция состояния системы, и ее изменение не зависит от пути проведения процесса,а зависит только от конечного и начального состояния системы.

ΔS=Sкон - Sнач

Дата добавления: 2018-02-28; просмотров: 946; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!