Изменение энтропии в различных процессах, при нагревании, фазовых переходах, расширении и смешении идеальных газов

⇐ ПредыдущаяСтр 5 из 40Следующая ⇒

Для реальных (необратимых) процессов II закон термодинамики записывается в идее неравенства, что затрудняет расчет Dизменения энтропии S при их протекании. Но энтропия – функция состояния системы, и ее изменение не зависит от пути проведения процесса. DПоэтому для расчета S при протекании различных процессов воспользуемся уравнением II закона для обратимых процессов:

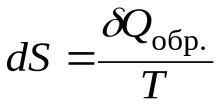. (1)

Изменение энтропии при фазовых превращениях

Фазовое превращение (фазовый переход) – процесс, связанный с изменением агрегатного состояния вещества.

Характерной особенностью этих процессов является то, что они протекают при постоянной температуре – температуре фазового перехода Т_ф.п.. (Т=const, изотермический процесс)

Тогда, согласно II закону термодинамики

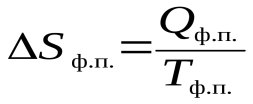где Q_ф.п. – тепловой эффект фазового перехода.

При р = const (изобарный процесс) теплота равна изменению энтальпии:

Изменение энтропии при нагревании (охлаждении).

Применим уравнение (1) к изобарному процессу (р = const).

Для 1 моль вещества

;

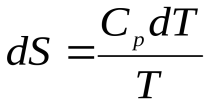где С_р – молярная изобарная теплоемкость K).×вещества, Дж/(моль (см. ниже)

Вычислим изменение энтропии для различных процессов:

1. В общем случае обратимого процесса при постоянном объеме, когда изменение внутренней энергии равно :

2. При нагревании любого вещества от 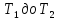при постоянном объеме (V=const, изохорный процесс). В случае, как следует из математической формулироквки первого начала термодинамики, теплота процесса приобретает свойства функции состояния и не зависит от пути процесса. Подставляя значение из уравнения и 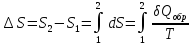, получаем:

Если принять

3. При нагревании любого вещества при постоянном давлении (p=const)

При (4)

4.Для различных процессов с идеальным газом:

Если , вместо уравнения (5) можно написать

Учитывая, что для идеального газа , уравнение (6) можно представить в виде:

В изотермическом процессе, учитывая, что получаем из (6) и (7)

В изохорном процессе, учитывая, что получаем из равенства (6)

В изобарном процессе, учитывая, что 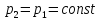и 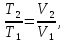находим из (7)

Смешение двух идеальных газов

При смешивании энтропия увеличивается. Причина: расширение каждого из газа при p=const и T=const.

, где n₁ и n₂ – числа моль первого и второго газа: V₁ и V₂ – их начальные объемы:

V= V₁ + V₂ - конечный объем.)

Постулат Планка. Расчет абсолютного значения энтропии газообразного вещества.

Возможность вычислить абсолютное значение энтропииположение, которое было сформулировано Планком (1912). Согласно этому положению, называемому постулатом Планкаэнтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю:

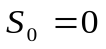(4.39)

Постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены, такие тела называются идеальными твердыми телами. Реальные кристаллы не являются таковыми. Поэтому реальные кристаллы при 0 К обладают энтропией больше нуля.

В соответствии с постулатом Планка уравнение для идеального твердого тела примет вид:

(4.40)

Можно показать, что при очень низких температурах не только энтропия и теплоемкость твердого тела стремятся к нулю (как это установлено экспериментально), но и многие другие свойства твердых тел (объем тела, давление насыщенного пара и др.) изменяются с температурой так, что их производные по температуре стремятся к нулю. Этим объясняется принцип недостижимости абсолютного нуля, согласно которому никакие процессы не могут снизить температуру тела до абсолютного нуля.

Постулат Планка используется при термодинамических расчетах химических процессов для вычисления абсолютных значений энтропий химических соединений. Энтропия твердого вещества вычисляется по уравнению (4.40). Для вычисления необходимо знать экспериментальные значения теплоемкостей, определенные для возможно низких температур до 10 К или 80 К. Значения теплоемкостей до 0 К находят путем экстраполяции по уравнениям Дебая или Тарасова либо с помощью эмпирических приемов.

Уравнение для вычисления энтропии газа при некоторой температуре будет иметь вид:

, (4.41)

где и _. – удельные теплоты агрегатных превращений.

Очевидно, что энтропию вещества, находящегося в жидком состоянии при температуре , также можно вычислить по уравнению (4.41), исключив два последних члена в правой части:

(4.42)

Дата добавления: 2018-02-28; просмотров: 11592; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!