Неустановившееся движение ЭП (переходные процессы, цели их рассмотрения, время переходного процесса, примеры)
Неустановившееся движение соответствует переходу ЭП из установившегося режима с одними параметрами в установившийся режим с другими параметрами.
Причины переходных процессов могут быть различны:
1. Изменение нагрузки  .
.
2. Изменение полезного момента двигателя 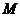 при пуске, торможении, реверсе.
при пуске, торможении, реверсе.
3. Изменение любого параметра системы ЭП.
Целью рассмотрения переходных процессов является получение зависимости изменения во времени выходных координат ЭП: 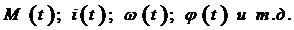
А так же определение времени переходного процесса 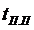 .
.
При изучении переходных процессов полагают, что известными являются следующие параметры:
1. Начальное состояние ЭП (  )
)
2. Конечное состояние ЭП ( 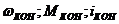 ) и соответствующая ему хар-ка
) и соответствующая ему хар-ка  .
.
3. Закон изменения во времени, факторы вызывающие переходный режим. Например 
4. Непосредственные параметры ЭП.
Переходные процессы в приводе можно условно разделить на четыре основные группы:
1. Переходные процессы в ЭП, где преобладающей инерционностью является момент инерции  . Электрические инерционности малы и не появляются, фактор вызывающий переходный процесс изменяется мгновенно. Примеры таких процессов: сброс, наброс нагрузки; пуск, торможение, реверс.
. Электрические инерционности малы и не появляются, фактор вызывающий переходный процесс изменяется мгновенно. Примеры таких процессов: сброс, наброс нагрузки; пуск, торможение, реверс.
2. Переходные процессы, когда механические и электрические инерционности соизмеримы, факторы, вызывающие переходный процесс, изменяются мгновенно.
3. Мех. и эл. инерционности малы, или не проявляются, а фактор вызывающий п.п. изменяется во времени.
|
|
|
4. Переходные процессы, когда учитываются все инерционности.
Рассмотрим различные переходные процессы, относящиеся к 1-й группе. Все эти переходные процессы можно описать основным уравнением движения ЭП.
 (1). При решении данного уравнения рассмотрим несколько случаев:
(1). При решении данного уравнения рассмотрим несколько случаев:
1. Пусть во время переходного процесса.  Привод работает в точке с координатами
Привод работает в точке с координатами  . В момент времени
. В момент времени  мгновенно переводится на новую хар-ку. В этом случае уравнение движения имеет вид
мгновенно переводится на новую хар-ку. В этом случае уравнение движения имеет вид 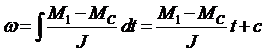 (2). Постоянная времени интегрирования
(2). Постоянная времени интегрирования  находится из условия:
находится из условия:  . Если подставить в уравнение (2), то
. Если подставить в уравнение (2), то  . Окончательное решение уравнения (2):
. Окончательное решение уравнения (2):  (3). Это решение действует на интервале:
(3). Это решение действует на интервале:  . Т.к. по условию при
. Т.к. по условию при  функция
функция  терпит излом. На интервале
терпит излом. На интервале  момент равен
момент равен 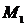 .
.
 Время
Время  определяем из выражения (3). Если подставить в него, то
определяем из выражения (3). Если подставить в него, то  (4). На основании выражения (4) можно сделать вывод, что при положительном динамическом моменте скорость увеличивается, при отрицательном скорость уменьшается.
(4). На основании выражения (4) можно сделать вывод, что при положительном динамическом моменте скорость увеличивается, при отрицательном скорость уменьшается.
 2. Момент нагрузки и полезный момент зависят от скорости:
2. Момент нагрузки и полезный момент зависят от скорости: 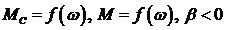
Уравнение механические хар-ки механизма и двигателя имеют вид:
 ,
,  - моменты двигателя и исполнительного механизма при нулевой скорости. Если в выражение (5) подставить уравнение (1), то получим:
- моменты двигателя и исполнительного механизма при нулевой скорости. Если в выражение (5) подставить уравнение (1), то получим: 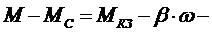

|
|
|
(6). После преобразований: 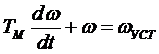 (7), где
(7), где  - электромеханическая постоянная времени,
- электромеханическая постоянная времени,  - установившееся значение скорости соответствующая точке пересечения хар-к двигателя и механизма. Выражение (7) решенное относительно времени имеет вид:
- установившееся значение скорости соответствующая точке пересечения хар-к двигателя и механизма. Выражение (7) решенное относительно времени имеет вид:  (8). Постоянный коэффициент А определяется из начального условия: при
(8). Постоянный коэффициент А определяется из начального условия: при  =>
=>  . Окончательное решение уравнения (7) имеет вид:
. Окончательное решение уравнения (7) имеет вид:  (9). На основании уравнения (5) момент двигателя можно записать:
(9). На основании уравнения (5) момент двигателя можно записать:  (10). Учитывая
(10). Учитывая  , получаем
, получаем  (11). Время
(11). Время  за которое измениться скорость от некоторого начального значения
за которое измениться скорость от некоторого начального значения 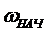 до конечного определяется по выражению:
до конечного определяется по выражению:  или для моментов
или для моментов 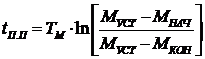
 Из (9) и (11) следует что
Из (9) и (11) следует что  и
и 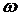 изменяются по экспоненциальному закону, т.е. теоретически
изменяются по экспоненциальному закону, т.е. теоретически  . По этому теоретически в технических расчетах пользуются временем
. По этому теоретически в технических расчетах пользуются временем  , считается, что за это время скорость достигает
, считается, что за это время скорость достигает  . Количественно
. Количественно  :
:  ,
,  - время разгона ЭП вхолостую (
- время разгона ЭП вхолостую (  ). Из неподвижного состояния (
). Из неподвижного состояния ( 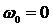 ) до скорости идеального холостого хода под действием пускового момента
) до скорости идеального холостого хода под действием пускового момента  . На практике:
. На практике:  ,
,  ,
,  .
.
3. АД. В зависимости от нагрузки и момента нелинейности.
1 – хар-ка АД, 2 – нагрузка (вентиляторная).
Для решения используем приближенный способ численного интегрирования уравнения движения. Используем метод Тейлора. Данный метод подразумевает замену дифференциала d на приращение  .
. 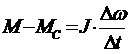 . Любую кривую можно заменить на ломанную.
. Любую кривую можно заменить на ломанную.  (*),
(*),  - зависит от хар-ра нагрузки и квадранта в котором работаем. Для пользования этим уравнением ось скорости разбиваем на участки, на каждом из которых момент АД и момент нагрузки считаем постоянными, причем интервалы
- зависит от хар-ра нагрузки и квадранта в котором работаем. Для пользования этим уравнением ось скорости разбиваем на участки, на каждом из которых момент АД и момент нагрузки считаем постоянными, причем интервалы 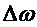 могут быть неравномерными.
могут быть неравномерными.
|
|
|
Дата добавления: 2018-02-15; просмотров: 661; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
