Время пуска и торможения ЭП. Угол поворота вала двигателя за время пуска и торможения.
Для определения продолжительности пуска или торможения необходимо решить основное уравнение движения ЭП относительно координаты время. Если принять, что в процессе пуска величины: суммарный момент инерции 
, полезного момента двигателя М, момента нагрузки 
остаются const, то время пуска определяется:
- угловая скорость вращения двигателя, соответствующая нагрузке 
.
Если 
, то время пуска определяется как 
.
При торможении с использованием тормозного момента время можно определить как:
.
- если торможение происходит только под действием нагрузки (торможение выбегом).
Если считать, что механика между двигателем и исполнительным органом абсолютно жесткая, то угол поворота вала определяется:
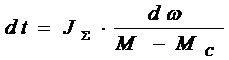
Т. к. время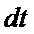 
увеличивается, тогда угол поворота вала за изменение скорости на величину 
.
Если принять, что величина динамического момента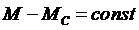 
, то угол поворота:
Если принять, что разгон идет от 0 скорости, т.е. 
до установившегося значения
, то
Устойчивость статического режима работы ЭП.
Статическому режиму работы соответствует движение всех элементов электромеханической системы с постоянной скоростью. Этот режим наступает после затухания переходных процессов, вызванных изменением управляющих или возмущающих воздействий и характеризуется равенством электромагнитного (полезного) момента двигателя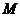 
и суммарный момент нагрузки
|
|
|
Это условие вытекает из условия уравнения движения ЭП. Если в нем принять 
или 
:
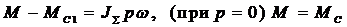Для одномассовой:
Для двухмассовой системы: 
Следовательно, основное условие статического режима работы выглядит: 
и определяется графически точкой пересечения хар-ки двигателя с мех. хар-кой механизма.
1, 2 – характеристики АД для различного направления движения;3 – активная нагрузка;4 – реактивная нагрузка; 5 – вентиляторная;
Если рассматривать активную нагрузку (3), то при 
дает пересечение с мех. характеристикой эл. двигателя в точке а ( 
). В этой точке двигатель работает в двигательном режиме преодолевая активный полезный момент и реактивный момент потерь. При 
хар-ка (3) пересекает хар-ку двигателя в точке b ( 
), где двигатель работает в тормозном режиме (рекуперативное торможение). В этой точке тормозной момент двигателя совместно с реактивным моментом механических потерь уравновешивает движ. момент полезной нагрузки.
Хар-ка 4 (реактивная нагрузка) пересекается с хар-кой АД при скоростях больше нуля в двух точках с и d, со скоростями 
и 
. В этих двух точках выполняется условие статического равновесия ( 
), устойчивым это равенство является только в точке с, при 
точка f. Незначительное отклонение скорости от 
(точка d) вниз дает уменьшение момента двигателя, следовательно, разница 
становится отрицательной, это вызывает появление тормозного динамического момента и как следствие дальнейшее уменьшение скорости.
|
|
|
При отклонении скорости в сторону увеличения к 
=> увеличивается момент двигателя 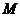, разница 
=> появляется динамический момент, который разгоняет привод, и мы переезжаем из точки d в точку c со скоростью . Берем точку с. Уменьшение скорости ниже уровня приводит к увеличению 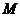, разница 
; 
и возвращаемся в точку с. В обратную сторону от с 
. Это справедливо для рабочего участка хар-ки двигателя. Условие возникновения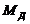 
при отклонении от точки статического равновесия зависит как от формы хар-ки машины, так и от вида хар-ки исполнительного механизма (нагрузки).
Например: Для примера с реактивной нагрузкой (4) точка d была неустойчива статическим режимом работы, а для вентиляторного хар-ра нагрузки (5), она является устойчивой. Т.к. при отклонении скорости в любую сторону момент нагрузки изменится более значительно, чем момент двигателя, что при любом отклонении возвращает систему точки 
. Из выше сказанного следует, что при постоянной нагрузке 
устойчивость статического режима работы зависит от знака жесткости механической характеристики двигателя.
|
|
|
Условия устойчивости. 
т.е. с увеличение нагрузки скорость должна падать.
Если момент механизма зависит от скорости следовательно его хар-ка обладает конечной жесткостью 
. При этом условии статическая устойчивость будет выглядеть: 
.
Дата добавления: 2018-02-15; просмотров: 821; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!