Решение. Данное уравнение является линейным неоднородным ДУ второго порядка с постоянными коэффициентами.
Составим и решим характеристическое уравнение: 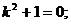
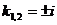 .
.
Тогда общее решение имеет вид: 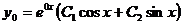

Частное решение неоднородного ДУ ищем в виде: 
Получаем: α=0, r=0, Q(x)=Ax+B.
Т.е.  ,
,  ,
, 

Ах+В=х, А=1, В=0; Т.о. 
Общее решение ДУ имеет вид: 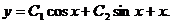
Ответ: 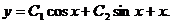
Пример 5. Решить уравнение: 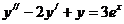
Решение. Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

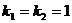 ;
;
Общее решение однородного уравнения:  .
.
Теперь найдем частное решение неоднородного уравнения в виде:
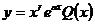

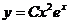 .
.
Воспользуемся методом неопределенных коэффициентов.
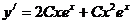 ;
;
 .
.
Подставляя в исходное уравнение, получаем:
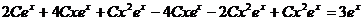 ;
;
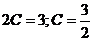 .
.
Частное решение имеет вид: 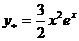 .
.
Общее решение линейного неоднородного уравнения:  .
.
Ответ: 
Пример 6. Найти общее решение дифференциального уравнения: 
Решение. Общее решение исходного уравнения, равного сумме общего решения однородного уравнения y0 и частного решения y* .
1. Найдем y0 . Находим корни характеристического уравнения:

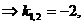

2. Найдем y* . Так как правая часть уравнения  , (α = 1 не является корнем характеристического уравнения, степень многочлена равна одному), то частное решение y* ищем в виде:
, (α = 1 не является корнем характеристического уравнения, степень многочлена равна одному), то частное решение y* ищем в виде: 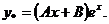
Находим

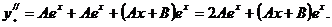
Подставляя y* , y*', y*" в исходное уравнение, получаем:
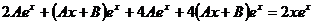
Разделив на ex , после приведения подобных слагаемых получим:
6A+9Ax+9B=2x.
Сравнивая коэффициенты при одинаковых степенях, составляем систему линейных алгебраических уравнений:

найдя решение этой системы: 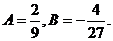
|
|
|
Записываем общее решение: 
Ответ: 
Пример 7. Найти общее решение дифференциального уравнения 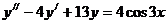
Решение. Общее решение ЛНДУ имеет вид y = yо+ y*.
1. Найдем у0. Решаем характеристическое уравнение 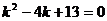 ,
, 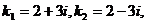 , следовательно,
, следовательно, 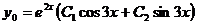 .
.
2. Найдем частное решение у*. Правая часть ЛНДУ имеет вид 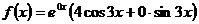 , т.е.
, т.е. 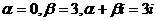 не совпадает с корнем характеристического уравнения, то r=0. Тогда частное решение находи в виде
не совпадает с корнем характеристического уравнения, то r=0. Тогда частное решение находи в виде 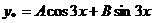 .
.

 .
.
Подставляя в уравнение, получаем

Упрощаем  .
.
Решаем систему уравнений:
 A=0,1, B=-0,3.
A=0,1, B=-0,3.
Следовательно,  .
.
Общее решение 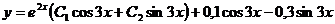
Ответ: 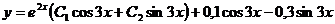
Практические задания
1. Решите уравнение методом понижения порядка
2. Найдите частное решение ДУ.
3. Решите однородное ДУ второго порядка.
4. Найдите общее решение неоднородного ДУ второго порядка.
5. Найдите общее решение неоднородного ДУ второго порядка.
| Вариант 1 1. y///=27sin(3x-5)+4 2. y//=2x, y(0)=0, y/(0)=1 3. y//+4y/-3y=0 4. y//-2y/+y=2х 5. y//-y/-6y=sin2x | Вариант 2 1. y///=16cos2x 2. y//=6x2, y(0)=0, y/(0)=2 3. y//-6y/+9=0 4. y//-3y/+2y=10е-х 5. y//-3y/-4y=cos4x |
| Вариант 3 1. y///=48x2-3 2. y//=sinx, y(0)=0, y/(0)=1 3. y//-4y/+3y=0 ‘ 4. y//-7y/+6y=sinx 5. y//-2y/-3y=e4x | Вариант 4
1. y//=24х-6
2. y//=  , y(1)=2, y/(1)=1
3. y//+4y/=0
4. 2y//+5y/=2cosx
5. y//-7y/+6y=sinx , y(1)=2, y/(1)=1
3. y//+4y/=0
4. 2y//+5y/=2cosx
5. y//-7y/+6y=sinx
|
Вариант 5
1. у///=sin2x
2. y//=  , y(0)=0, y/(0)=1
3. y//+6y/+9y=0
4. y//-2y/-8y=2sin2x
5. y//-5y/+6y=6x2 , y(0)=0, y/(0)=1
3. y//+6y/+9y=0
4. y//-2y/-8y=2sin2x
5. y//-5y/+6y=6x2
| Вариант 6
1. у///=81sin3x
2. y//= 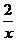 , y(1)=4, y/(1)=1
3. y//+y/+y=0
4. y//+25y/=cos5x
5. y//-y/-12y=x-5 , y(1)=4, y/(1)=1
3. y//+y/+y=0
4. y//+25y/=cos5x
5. y//-y/-12y=x-5
|
Вариант 7
1. у///=32cos2x
2. y//= 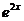 , y(0)=0, y/(0)=1
3. 2y//-3y/+y=0
4. y//+7y/+6y=cosx
5. y//-6y=x2-x , y(0)=0, y/(0)=1
3. 2y//-3y/+y=0
4. y//+7y/+6y=cosx
5. y//-6y=x2-x
| Вариант 8 1. у///=2cos(2x-1) 2. у//=x-3, y(0)=2, y/(0)=1 3. y//-2y/+2y=0 4. y//-y/-6y=3sinx 5. y//-y/=e-2x |
| Вариант 9 1. у///=12sin(3x+4) 2. y//=e-x, y(0)=3, y/(0)=2 3. y//+3y/+y=0 4. y//-2y/-8y=e2x 5. y//+9y=6cos2x | Вариант 10 1. у///=9cos2x-2 2. y//=2-x, y(1)=0, y/(0)=2 3. y//-6y/+45y=0 4. y//+2y/+5y=cos2x 5. y//-2y/-35y=xex |
| Вариант 11 1. у///=64cos4x+5x 2. y//=3x+1, y(0)=3, y/(0)=4 3. y//+y/+y=0 4. y//+y/-20y=e-2x 5. y//+8y=sin4x | Вариант 12 1. у///=125sin5x+3 2. y//=-2x-1, y(0)=1, y/(0)=2 3. y//+4y/+8y=0 4. y//-8y/+16y=4sinx 5. y//-5y/+4y=x2-3x |
| Вариант 13 1. у///=36cos6x-3x2 2. y//=4x-1, y(1)=3, y/(1)=2 3. y//-2y/+y=0 4. y//-7y/+10y=4e3x 5. y//-3y/=sin5x | Вариант 14 1. у///=100sin10x+x 2. y//=5x+2, y(0)=4, y/(0)=1 3. y//+2y/+5y=0 4. y//-7y/=x-2 5. y//+8y/+7y=-cos3x |
Контрольные вопросы:
|
|
|
1. Что называется дифференциальным уравнением n-го порядка?
2. Какой вид имеет дифференциальное уравнение, допускающее понижение порядка? Алгоритм решения таких уравнений.
3. Какой вид имеет линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами?
4. Что такое характеристическое уравнение?
5. Какой имеет вид общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, если корни характеристического уравнения: а) действительные и различные; б) действительные и равные? в) комплексные сопряженные?
|
|
|
6. Какой имеет вид общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами?
3 вариант
| 4 вариант
|
Вариант 5
| Вариант 6
|
Вариант 7
| Вариант 8
|
Вариант 9
| Вариант 10
1. 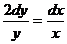 2.
2.  , если у=0 при х=1
3. , если у=0 при х=1
3.  4. у///=9cos2x-2
5. y//-6y/+45y=0
4. у///=9cos2x-2
5. y//-6y/+45y=0
|
Вариант 11
| Вариант 12
|
Вариант 13
| Вариант 14
|
Вариант 11
6. ydy=exdx
7. 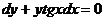 , если у=1 при х=0.
8. xy/+y=3
9. у///=64cos4x+5x
10. y//+y/+y=0 , если у=1 при х=0.
8. xy/+y=3
9. у///=64cos4x+5x
10. y//+y/+y=0
| Вариант 12 6. x3dx=(3-y)dy 7. y2dx=exdy, если у=1 при х=0. 8. xy/-3y=x4ex 9. у///=125sin5x+3 10. y//+4y/+8y=0 |
Вариант 13
6.  7. 1+y2=xyy/, y(2)=1
8. xy/-y-x3=0
9. у///=36cos6x-3x2
10. y//-2y/+y=0
7. 1+y2=xyy/, y(2)=1
8. xy/-y-x3=0
9. у///=36cos6x-3x2
10. y//-2y/+y=0
| Вариант 14 6. y/+y=5 7. cosxsinydy=cosysinxdx, y(π)=π. 8. y/-3xy=2xy2 9. у///=100sin10x+x 10. y//+2y/+5y=0 |
|
|
|
Дополнительная глава
Несобственные интегралы
Пусть дана функция y=f(x) непрерывная на интервале 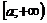 .
.
Рассмотрим интеграл  . Т.к. функция f(x) непрерывна, то он имеет смысл при любом b>a. Интерес вызывает интеграл при
. Т.к. функция f(x) непрерывна, то он имеет смысл при любом b>a. Интерес вызывает интеграл при  .
.
Определение. Если существует конечный предел  , то этот предел называется несобственным интегралом от функции f(x) на интервале
, то этот предел называется несобственным интегралом от функции f(x) на интервале 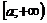 и обозначается
и обозначается  .
.
Следовательно, по определению имеем:
 . (1)
. (1)
В данном случае говорим, что несобственный интеграл  существует или сходится. Если
существует или сходится. Если  при
при  не имеет конечного предела, говорят, что
не имеет конечного предела, говорят, что  не существует или расходится.
не существует или расходится.
Выясним геометрический смысл несобственного интеграла. Как уже знаем  , где f(x)
, где f(x)  есть площадь криволинейной трапеции, ограниченной графиком функции f(x), линиями x=a, x=b и осью Ох (рис2). Не трудно догадаться, что
есть площадь криволинейной трапеции, ограниченной графиком функции f(x), линиями x=a, x=b и осью Ох (рис2). Не трудно догадаться, что  выражает площадь неограниченной области, заключенной между линиями y=f(x), x=a и осью абсцисс (рис.3).
выражает площадь неограниченной области, заключенной между линиями y=f(x), x=a и осью абсцисс (рис.3).
Аналогично можно рассмотреть интеграл 
 при
при 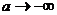 , тогда
, тогда 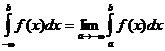 . (2)
. (2)
Несобственный интеграл  можно определить как сумму двух интегралов:
можно определить как сумму двух интегралов:
 , (3)
, (3)
где с—любое число при условии существования обоих интегралов справа.
Рассмотрим случай, когда функция y=f(x) определена и непрерывная на промежутке 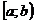 , а в т. x=b функция либо не определена, либо терпит разрыв (рис.4).
, а в т. x=b функция либо не определена, либо терпит разрыв (рис.4).
 от функции f(x), разрывной в т. с, определяется следующим образом:
от функции f(x), разрывной в т. с, определяется следующим образом:
 .
.
Если предел, стоящий справа, существует, то несобственный интеграл называется сходящимся. В противном случае интеграл называется расходящимся.
Если функция f(x) определена и непрерывна на промежутке 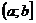 , т.е. терпит бесконечный разрыв в т. х=a, то аналогично имеем:
, т.е. терпит бесконечный разрыв в т. х=a, то аналогично имеем:
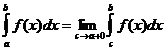 .
.
Если же функция f(x) имеет точку разрыва внутри отрезка 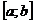 , например в т. х=с, то
, например в т. х=с, то  можно представить в виде суммы двух несобственных интегралов:
можно представить в виде суммы двух несобственных интегралов:
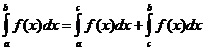 .
.
Практическая часть.
Пример 1. Найти значение или установить расходимость несобственного интеграла 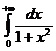 .
.
Решение. По определению собственного интеграла (1) имеем:

Ответ: 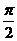 .
.
Пример 2. Найти значение или установить расходимость несобственного интеграла  .
.
Решение. По определению собственного интеграла (1) имеем:
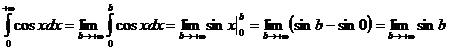 .
.
Т.к. данный предел не существует, несобственный интеграл расходится.
Ответ. Интеграл расходится.
Пример 3. Вычислить интеграл 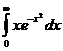 .
.
Решение. Подынтегральная функция определена и непрерывна при всех значениях х и, следовательно, имеет первообразную 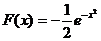 .
.
По определению имеем:  .
.
По формуле Ньютона-Лейбница,
 ;
;
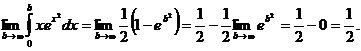
Пример 4. Найти значение или установить расходимость несобственного интеграла
 .
.
Решение. Представим данный интеграл в виде суммы двух несобственных интегралов:
 .
.
Вычислим первый интеграл: 
Второй интеграл мы уже находили (см. Пример 1) и равен также 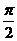 .
.
Т.о. 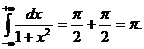
Ответ: π.
Пример 5. Найти значение или установить расходимость несобственного интеграла  .
.
Решение. Функция f(x)=  имеет точку разрыва х=0 внутри отрезка
имеет точку разрыва х=0 внутри отрезка 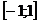 . (см. рис 5).
. (см. рис 5).
Поэтому представим интеграл в виде суммы двух интегралов:
 . Вычислим каждый интеграл отдельно:
. Вычислим каждый интеграл отдельно:
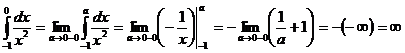 , следовательно, интеграл на отрезке
, следовательно, интеграл на отрезке 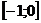 расходится.
расходится.
Аналогично можно найти, что  , следовательно, интеграл расходится на отрезке
, следовательно, интеграл расходится на отрезке  . Т.о. интеграл расходится на отрезке
. Т.о. интеграл расходится на отрезке 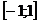 .
.
Ответ. Интеграл расходится.
Дата добавления: 2018-02-18; просмотров: 1349; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

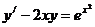
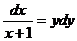 .
. y3dx=0, если у=1 при х=-1.
y3dx=0, если у=1 при х=-1. .
. если у=1 при х=-1
если у=1 при х=-1 dx
dx
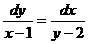 , если у=4 при х=0
, если у=4 при х=0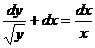 , если у=1 при х=1.
, если у=1 при х=1.