Что называется областью определения функции двух переменных?

Дайте определение предела функции двух переменных.

Какая функция называется непрерывной в точке?

Что называется частным производным функции от переменной х? у?

Как найти полный дифференциал функции?

Способы нахождения производной неявной функции.

Практическая работа №19

Вычислить двойных интегралов в случае области 1 и 2 »

Цель работы: сформировать навыки нахождения двойных интегралов в прямоугольных координатах, применения двойных интегралов для решения геометрических задач.

Теоретическая часть

Пусть функция f(x,y) определена внутри некоторой области D и на ее границе. Разобьем область D на n частичных областей D₁, D₂, ..., D_n. Их площади обозначим через ∆S₁,∆S₂,…,∆S_n. В каждой частичной области возьмем по произвольной точке (P₁(x₁; y₁) в области D₁, P₂ (x₂; y₂) в области D₂ , и т.д.). Составим интегральную сумму:

Обозначим через d наибольший из диаметров области D. Устремим n к бесконечности так, чтобы d стремилось к нулю.

Рис.1

Конечный предел последовательности S_n (если он существует) при d → 0 , который не зависит ни от способа разбиения области D , ни от выбора точек P₁, P₂, ..., P_n, называется двойным интегралом функции f(x,y) и обозначается

Функция f(x,y) называется интегрируемой функцией на области D . Область D называется областью интегрирования.

Непрерывная на замкнутой области функция является интегрируемой на этой области.

Геометрический смысл двойного интеграла. Пусть интегрируемая функция f(x,y) принимает в области D только положительные значения. Тогда двойной интеграл численно равен объему вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности z = f(x,y).

повторном интеграле. (см. рис. 1)

Свойства двойного интеграла

Свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла.

1. Двойной интеграл от алгебраической суммы функции равен алгебраической сумме двойных интегралов от слагаемых функций:

3. Постоянный множитель можно вынести за знак двойного интеграла:

4. Если в области D , то

5. Если область D представляется в виде объединения двух областей D₁ и D₂ ,без общих внутренних точек, то

6. Теорема о среднем значении.

Если функция f(x,y) непрерывна на области D, то существует точка М₀(х₀,у₀) 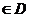такая, что

Вычисление двойного интеграла

1) Если граница области D пересекается всякой прямой x = c (c - const) не более чем в двух точках, то область D называется правильной в направлении оси OX. Ограниченная область D , правильная в направлении оси ОХ, задается неравенствами:

a ≤ x ≤ b, φ₁(x) ≤ y ≤ φ₂(x),

где φ₁(x), φ₂(x) - функции, непрерывные на отрезке [a, b] (рис.2).

В этом случае двойной интеграл выражается через повторный интеграл по формуле

(1)

Сначала необходимо найти определенный интеграл 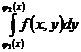по переменной у предполагая, что х остается постоянным. Затем результат интегрируется по переменной х.

Рис.2 рис.3

2). Если граница области D пересекается прямой y = c (c постоянная) не более чем в двух точках, то область D можно задать другими неравенствами:

. (рис.3)

В этом случае двойной интеграл выражается через повторный интеграл по формуле

(2)

где интегрирование сначала выполняется по переменной х, а затем у.

3).Если область D есть прямоугольник со сторонами параллельными координатным осям и заданными неравенствами (рис.4), то двойной интеграл вычисляется по формуле

или (3)

. Рис. 4

Двойные интегралы используется при решении многих геометрических и физических задач: вычисление площадей плоских фигур и поверхностей, объемов тел, координат центра тяжести, массы плоской фигуры, статистических моментов плоской фигуры, моментов инерции и т.д. Остановимся только на некоторых.

Дата добавления: 2018-02-18; просмотров: 890; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!