Что называется областью интегрирования?
В чем состоит геометрический смысл двойного интеграла?
Перечислите свойства двойного интеграла.
Вычисление двойного интеграла, если областью интегрирования прямоугольник.
Вычисление двойного интеграла в области 1 и 2.
Практическая работа №20
«Исследование сходимости знакоположительных рядов»
Цель работы: сформировать навыки исследования числовых рядов на сходимость.
Теоретическая часть
Определение. Сумма членов бесконечной числовой последовательности
a1, a2, a3,…, an, …
называется числовым рядом и обозначается
 (1)
(1)
При этом числа a1, a2, a3,…, an, называются членами ряда, а  – общим членом ряда.
– общим членом ряда.
Ряд считается заданным, если задано правило, позволяющее по известному номеру n его члена записать этот член ряда.
Определение. Сумма первых n членов ряда называется n-ой частичной суммойряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение. Ряд  называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.


Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакое числовое значение.
Необходимый признак сходимости числового ряда (1):
|
|
|
Если ряд (1) сходится, то предел его общего члена равен нулю:

Отсюда вытекает, что если  , то ряд расходится. Но выполнение необходимого признака сходимости не гарантирует сходимость данного ряда и следует исследовать ряд с помощью достаточных признаков сходимости.
, то ряд расходится. Но выполнение необходимого признака сходимости не гарантирует сходимость данного ряда и следует исследовать ряд с помощью достаточных признаков сходимости.
Достаточные признаки сходимости рядов с положительными членами
Определение. Ряд 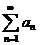 , у которого все a1>0, a2>0,..., an>0,... называется знакоположительным числовым рядом.
, у которого все a1>0, a2>0,..., an>0,... называется знакоположительным числовым рядом.
Рассмотрим два знакоположительных числовых ряда:
 (2)
(2)
 (3)
(3)
Признак сравнения I. Пусть даны два числовых ряда (2) и (3). Исследуется на сходимость ряд (2). Известно поведение ряда (3). Если начиная с некоторого номера n:
1) an ≤ bn - члены ряда (2) не больше соответствующих членов ряда (3), и ряд (3) сходится, то и ряд (2) также сходится.
2) an ≥ bn - члены ряда (2) не меньше соответствующих членов ряда (3), и ряд (3) расходится, то и ряд (2) также расходится.
Сравнение исследуемых рядов производится обычно со следующими известными рядами:
1)  , a ≠ 0 (геометрическая прогрессия, сходящаяся при |q| < 1 и расходящаяся при |q| ≥ 1);
, a ≠ 0 (геометрическая прогрессия, сходящаяся при |q| < 1 и расходящаяся при |q| ≥ 1);
2)  расходящийся гармонический ряд;
расходящийся гармонический ряд;
3)  (обобщенный гармонический ряд, сходящийся при p > 1 и p ≤ 1).
(обобщенный гармонический ряд, сходящийся при p > 1 и p ≤ 1).
|
|
|
Признак сравнения II. Пусть даны два числовых ряда (2) и (3). Исследуется на сходимость ряд (2). Известно поведение ряда (3). Если существует конечный предел 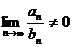 , то оба ряда (2) и (3) либо одновременно сходятся, либо одновременно расходятся. Если же
, то оба ряда (2) и (3) либо одновременно сходятся, либо одновременно расходятся. Если же  , то из сходимости ряда (3) следует сходимость ряда (2).
, то из сходимости ряда (3) следует сходимость ряда (2).
2 Признак Даламбера
Пусть дан ряд (2) с положительными членами. Допустим, что  существует и
существует и
 .
.
Тогда: 1) если ρ<1, то ряд (1) сходится;
2) если ρ>1,то ряд (1) расходится.
При ρ=1 требуется дополнительное исследование.
3 Признак Коши
Замечание. Признак Даламбера целесообразно применять тогда, когда общий член ряда содержит факториал или содержит одновременно степенную и показательную функции относительно n.
Признак Коши (радикальный). Пусть дан числовой ряд (2). Если существует предел  , то
, то
при k < 1 ряд (2) сходится,
при k > 1 ряд (2) расходится,
при k = 1 вопрос о сходимости ряда (2) остается открытым.
Замечание. Признак Коши (радикальный) целесообразно применять в том случае, если общий член ряда представляет собой n-ю степень некоторого выражения.
Интегральный признак Коши (основан на сравнении рядов с несобственными интегралами). Пусть общий член ряда (2) an = f(n) > 0. Если функция f(x), принимающая в точках x = n, n = 1, 2, 3, ... значения f(n), монотонно убывает в некотором интервале A<x<∞, где A>1, то числовой ряд 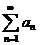 и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
|
|
|
Практическая часть
Пример 1. Исследовать на сходимость ряд  .
.
Решение
 .
.
Т.е. необходимый признак сходимости не выполнен.
Ответ: ряд  расходится.
расходится.
Пример 2. Исследовать на сходимость ряд  .
.
Решение.Так как n>lnn для n≥2, тогда 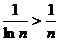 для
для  , а
, а  - общий член расходящегося гармонического ряда, то в силу признака сравнения I данный ряд расходится.
- общий член расходящегося гармонического ряда, то в силу признака сравнения I данный ряд расходится.
Ответ: ряд  расходится.
расходится.
Пример 3. Исследовать ряд  на сходимость по признаку Даламбера.
на сходимость по признаку Даламбера.
Решение. 
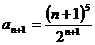 .
.

 . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Ответ: ряд  сходится.
сходится.
Пример 4. Исследовать на сходимость ряд  .
.
Решение.Применяем признак Даламбера. По известному члену ряда an, заменяя в нем n на n + 1, находим следующий за ним член an+1. Здесь
 ,
, 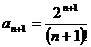 ,
,

следовательно, ряд сходится.
Ответ: ряд  сходится.
сходится.
Пример 5. Исследовать на сходимость ряд  .
.
Решение. Общий член ряда представляет собой n-ю степень некоторого выражения, поэтому удобнее всего применение радикального признака Коши:

следовательно, ряд расходится.
Ответ: ряд  расходится.
расходится.
|
|
|
Практические задания
1 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
| 2 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1. 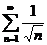 2.
2.  3.
3.  4.
4. 
|
3 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
| 4 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  .
4. .
4. 
|
5вариант
1. Найдите первые четыре члена ряда
  2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
| 6 вариант
1. Найдите первые четыре члена ряда
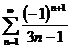 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
|
7 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2. 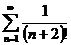 3.
3.  4.
4. 
| 8 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.   4.
4. 
|
9 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
| 10 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
|
11 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость
1.
2. Исследовать ряды на сходимость
1.  2.
2.  3.
3.  4.
4. 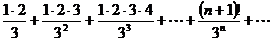 5.
5. 
| 12 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2.  3.
3.  4.
4. 
|
13 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2. 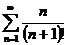 3.
3.  4.
4. 
| 14 вариант
1. Найдите первые четыре члена ряда
 2. Исследовать ряды на сходимость:
1.
2. Исследовать ряды на сходимость:
1.  2.
2. 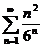 3.
3.  4.
4. 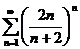
|
Контрольные вопросы:
Дата добавления: 2018-02-18; просмотров: 972; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
