Что называется числовым рядом?
Что называется суммой числового ряда?
Дайте определение сходящегося ряда.
Сформулируйте необходимое условие сходимости числового ряда.
5. Сформулируйте достаточные признаки знакоположительных рядов:
a) Признаки сравнения;
b) Признак Даламбера;
c) Признак Коши;
D) Интегральный признак Коши.
Что называется гармоническим рядом? Обобщенным гармоническим рядом?
Практическая работа №21
«Исследование сходимости знакочередующихся рядов»
Цель работы: Сформировать навыки исследования знакопеременных рядов на сходимость.
Теоретическая часть
Определение. Ряд 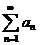 , (1)
, (1)
содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Определение. Знакопеременный ряд (1) называется абсолютно сходящимся, если сходится ряд  , (2)
, (2)
составленный из модулей членов данного ряда.
Естественно, что всякий абсолютно сходящийся ряд является сходящимся, т. е. из сходимости ряда (2) всегда следует сходимость ряда (1).
Определение. Знакопеременный ряд (1) называется условно сходящимся, если он сходится, а ряд (2), составленный из модулей его членов, расходится.
Исследовать на сходимость знакопеременный ряд - значит не только ответить на вопрос, сходится он или расходится, но и как сходится: абсолютно или условно.
|
|
|
Среди знакопеременных рядов особо выделяют класс знакочередующихся рядов.
Определение. Знакочередующимся называется ряд, в котором два соседних члена имеют разные знаки. Его можно записать так:
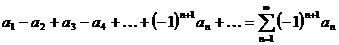
или (3)

Для знакочередующихся рядов справедлив следующий достаточный признак сходимости.
Признак Лейбница. Пусть дан знакочередующийся ряд (3). Если выполнены два условия:
1)  - (члены, начиная с некоторого, монотонно убывают по абсолютной величине);
- (члены, начиная с некоторого, монотонно убывают по абсолютной величине);
2) 
то ряд (3) сходится.
Всякий абсолютно сходящийся ряд есть ряд сходящийся.
При исследовании знакопеременных рядов на абсолютную сходимость пользуются всеми известными признаками сходимости для рядов с положительными членами.
Практическая часть
Пример 1. Используя признак Лейбница, исследоватьна сходимость знакочередующийся ряд 
Решение. Т.к.1)  данный ряд расходится.
данный ряд расходится.
Ответ: ряд расходится
Пример 2. Исследовать на сходимость знакочередующийся ряд 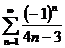 .
.
Решение.Применяем признак Лейбница. Так как
1)  - члены ряда монотонно убывают по абсолютной величине,
- члены ряда монотонно убывают по абсолютной величине,
2)  - выполнен необходимый признак, данный ряд сходится.
- выполнен необходимый признак, данный ряд сходится.
|
|
|
Исследуем ряд, составленный из модулей его членов  . Применим признак сравнения. Сравним данный ряд с рядом
. Применим признак сравнения. Сравним данный ряд с рядом  . Так как
. Так как  - гармонический ряд, про который известно, что он расходится, то и ряд полученный умножением ряда на константу также является расходящимся. 4n-3<4n,
- гармонический ряд, про который известно, что он расходится, то и ряд полученный умножением ряда на константу также является расходящимся. 4n-3<4n,  . Следовательно из расходимости рядя
. Следовательно из расходимости рядя  следует и расходимость ряда
следует и расходимость ряда  .
.
Ответ: ряд 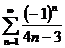 сходится условно.
сходится условно.
Пример 3. Исследовать на сходимость знакочередующийся ряд  .
.
Решение.Исследуем данный знакочередующийся ряд сразу на абсолютную сходимость. С этой целью составим ряд из модулей членов данного ряда:  . Применим к этому ряду признак Даламбера:
. Применим к этому ряду признак Даламбера:

 ,
,

Т.к. 0<1, ряд сходится
Здесь использован 2-й замечательный предел  .
.
Ряд из модулей сходится. Следовательно, исходный ряд сходится абсолютно.
Ответ: ряд  сходится абсолютно.
сходится абсолютно.
Пример 4.Исследовать на сходимость ряд 
Решение.Составим ряд из модулей данного ряда:

Этот ряд есть бесконечно убывающая геометрическая прогрессия и, следовательно, ряд сходится. Т.о. ряд сходится абсолютно.
Ответ: ряд сходится абсолютно.
Практические задания
Исследовать на сходимость знакочередующий ряд.
1. Выпишите первые пять членов ряда
|
|
|
2. Используя признак Лейбница, исследуйте сходимость знакочередующихся рядов.
3. Исследуйте на абсолютную и условную сходимость ряд
Вариант 1
1. 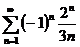 2. а)
2. а)  б)
б)  3. а)
3. а) 
|   Вариант 2
1. Вариант 2
1.  2. а)
2. а)  б)
б)  3. а)
3. а) 
|
Вариант 3
1.  2. а)
2. а)  б)
б)  3.
3. 
| Вариант 4
1.  2. а)
2. а)  б)
б)  3.
3. 
|
Вариант 5
1.  2. а)
2. а)  б)
б)  3.
3. 
| Вариант 6
1. 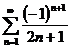 2. а)
2. а)  б)
б)  3.
3. 
|
Вариант 7
1.  2. а)
2. а)  б)
б)  3.
3. 
| Вариант 8
1.  2. а)
2. а)  б)
б)  3.
3. 
|
Вариант 9
1.  2. а)
2. а)  б)
б)  3.
3. 
| Вариант 10
1.  2. а)
2. а)  б)
б)  3.
3. 
|
Вариант 11
1.  2. а)
2. а) 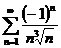 б)
б)  3.
3. 
| Вариант 12
1. 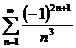 2. а)
2. а)  б)
б)  3.
3. 
|
Вариант 13
1. 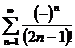 2. а)
2. а)  б)
б)  3.
3. 
| Вариант 14
1.  2. а)
2. а)  б)
б)  3.
3. 
|
Контрольные вопросы:
1. Какой ряд называется знакопеременным?
2. Какой ряд называется знакочередующимся?
3. Что называется абсолютно сходящимся рядом?
4. Что называется условно сходящимся рядом?
5. Сформулируйте признак Лейбница для знакочередующихся рядов.
Практическая работа №22
«Нахождение радиуса и области сходимости ряда. Разложение функции в ряд Маклорена»
Цель. Сформировать навыки исследования степенных рядов на сходимость.
Теоретическая часть
Пусть u1(x), u2(x), u3(x),…,un(x) – некоторая последовательность функций.
|
|
|
Выражение вида  u1(x)+u2(x)+…+un(x)+… называется функциональным рядом.
u1(x)+u2(x)+…+un(x)+… называется функциональным рядом.
Определение.Степенным рядом называется функциональный ряд вида
 (1)
(1)
Где х—независимая переменная,  --постоянные коэффициенты, а0 – фиксированное число.
--постоянные коэффициенты, а0 – фиксированное число.
Степенным рядом такженазывают ряд вида
 (2)
(2)
Он является частным случаем ряда (1) (a=0).
Теорема (Абеля). Если степенной ряд  сходится в точке х0,, то он абсолютно сходится в точке х, для которой
сходится в точке х0,, то он абсолютно сходится в точке х, для которой  .
.
Определение. Интервал (x0-R, x0+R), внутри которого ряд сходится, а вне его - расходится, называется интервалом сходимости, а число R - радиусом сходимости степенного ряда. Радиус сходимости степенного ряда можно вычислять по одной из формул
 или
или  (3)
(3)
при условии, что пределы, в них входящие, существуют.
Замечание. Для ряда (2) интервалом сходимости является (-R;R).
Исследовать степенной ряд на сходимость - значит, найти интервал его сходимости и выяснить, сходится или расходится ряд в граничных точках интервала сходимости.
В результате исследования рядов может получиться что:
1. R=0. Это означает, ряд сходится только при х=0.
2. R=  . Это означает, ряд сходится на всей числовой прямой, т.е.
. Это означает, ряд сходится на всей числовой прямой, т.е. 
3. R—Число отличное от нуля. В данном случае областью сходимости может быть один из нижеперечисленных вариантов:

Дата добавления: 2018-02-18; просмотров: 1300; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
