Вычисление площадей плоских фигур с помощью определенного интеграла

Рассмотрим несколько случаев применения определенного интеграла для нахождения площадей плоских фигур.

1. Пусть на отрезке [a;b] дана непрерывная неотрицательная функция y=f(x).

представляет собой площадь криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми х=а, х=b и осью Ох. В этом и состоит геометрический смысл определенного интеграла.

Т.е. (1)

2. Фигура ограничена графиком непрерывной неположительной функции, прямыми х=а, х=b и осью Ох. Тогда (2)

4. Фигура ограничена графиками двух непрерывных на отрезке функциями y=f(x) и y=g(x) и прямыми х=а, х=b, где . Тогда

(3)

4. Фигура прилегает к оси ординат и ограничена непрерывной кривой x=f(y), прямыми х=а, х=b и осью Оу. Тогда (4)

Объем тел вращения.

Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса , то объем тела вращения может быть легко найден по полученной выше формуле:

(5)

Если же необходимо найти объем тела, полученного вращением графика непрерывной на отрезке [a, b] функции у=f(x) вокруг оси Оу, то применяем формулу (6)

d y=f(x)

Вычисление пути, пройденного точкой

Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция временны t, то путь пройденный точкой за промежуток времени , вычисляется по формуле

(7)

Работа переменной силы

Если переменная сила F=F(x) действует в направлении оси Ох, то работа силы на отрезке вычисляется по формуле

(8)

Практическая часть

Пример 1. вычислить площадь тела ограниченной области, лежащей между графиками и .

Решение. Построим графики данных функции по точкам. Эти графики имеют две общих

точек. х₁ =0, х₂=1. При этом график функции находится выше графика функции (см. рисунок).

Значит, по формуле (3) площадь области между графиками равна

Пример 2. Вычислить объем тела, полученного от вращения графика функции

[1;3] вокруг оси Ох.

Решение. Используем формулу (5)

Пример 3. Скорость движения точки изменяется по закону v=(t²+4t-2) м/с. Найдите путь пройденный точкой за 6с от начала движения.

Решение. По условию f(x)=(t²+4t-2), t₁=0, t₂=6. По формуле (7) имеем:

Пример 4. Вычислите работу, произведенную при сжатии пружины на 0,03 м, если для сжатия ее на 0,02 м нужна сила 10 Н.

Решение. Согласно закону Гука F=kx. Т.к. х=0,02 при F=10Н, то

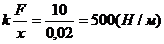. Подставляя значение k в закон Гука, имеем: f(x)=500x.

По формуле (8) имеем:

(Дж)

Практические задания

Вариант №1 1. Найдите площадь фигуры, ограниченной линиями: а) б) . 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=6, у=0,5х+4 и у=0. 3. Скорость движения точки изменяется по закону v=(2t²+3t-1) м/с. Найдите путь пройденный точкой за 10с от начала движения. 4. Вычислите работу, произведенную при сжатии пружины на 0,06 м, если для сжатия ее на 0,01 м нужна сила 10 Н.	Вариант №2 1. Найдите площадь фигуры, ограниченной линиями: а)2x-y+3=0, y=0, x=3, x=1 б) 2. Часть синусоиды y=sinx вращается вокруг оси Ох. Найдите объём тела вращения от до 3. Скорость движения точки изменяется по закону v=(12t-3t²) м/с. Найдите путь пройденный точкой от начала движения до ее остановки. 4. Вычислите работу, произведенную при сжатии пружины на 0,04 м, если для сжатия ее на 0,02 м нужна сила 40 Н.
Вариант №3 1. Найдите площадь фигуры, ограниченной линиями: a) y=x², y=0, x=1, x=3. б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у²=6х, у=1, х=1, х=3. 3. Скорость движения точки изменяется по закону v=(4t²+3t+1) м/с. Найдите путь пройденный точкой за 4-ую секунду. 4. Вычислите работу, произведенную при сжатии пружины на 0,08 м, если для сжатия ее на 0,02 м нужна сила 20 Н.	Вариант №4 1. Найдите площадь фигуры, ограниченной линиями: a) б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=3, х+у-3=0 и у=0. 3. Скорость падающего в пустоте тела изменяется по формуле V=9,8t. Какой путь пройдет тело за первые 10 с падения? 4. Вычислите работу, произведенную при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 30 Н.
Вариант №5 1. Найдите площадь фигуры, ограниченной линиями: a) б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=1, х=4, у-х+4 и у=0. 3. Скорость движения точки изменяется по закону v=(5t²-t-1) м/с. Найдите путь пройденный точкой за 8 с от начала движения. 4. Вычислите работу, произведенную при сжатии пружины на 0,1 м, если для сжатия ее на 0,02 м нужна сила 60 Н.	Вариант №6 1. Найдите площадь фигуры, ограниченной линиями: a) y=x³, y=0, x=-2, x=2. б) 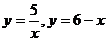2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=х²-4, у=0. 3. Скорость движения точки изменяется по закону v=(2t-4t²) м/с. Найдите путь пройденный точкой от начала движения до ее остановки. 4. Вычислите работу, произведенную при сжатии пружины на 0,12 м, если для сжатия ее на 0,02 м нужна сила 50 Н.
Вариант №7 1. Найдите площадь фигуры, ограниченной линиями: а) . б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=sinx, y=0, x=0, x=π. 3. Скорость движения точки изменяется по закону v=(3t²+2t-1) м/с. Найдите путь пройденный точкой за 5-ую секунду. 4. Вычислите работу, произведенную при сжатии пружины на 0,2 м, если для сжатия ее на 0,04 м нужна сила 10 Н.	Вариант №8 1. Найдите площадь фигуры, ограниченной линиями: а) y=-x²+x+6, y=0. б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями х=0, х=3, у=х-3 и у=0. 3. Скорость падающего в пустоте тела изменяется по формуле V=9,8t. Какой путь пройдет тело за первые 5 с падения? 4. Вычислите работу, произведенную при сжатии пружины на 0,06 м, если для сжатия ее на 0,03 м нужна сила 60 Н.
Вариант №9 1. Найдите площадь фигуры, ограниченной линиями: а)y=2cosx, б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями y²=4x, y=0, х=0, х=4 3. Скорость движения точки изменяется по закону v=(3t-t²+4) м/с. Найдите путь пройденный точкой за 5с от начала движения. 4. Вычислите работу, произведенную при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 30 Н.	Вариант №10 1. Найдите площадь фигуры, ограниченной линиями: а) xy=4, x=4, x=8. б) y=2+4x-x², y=x²-2x+2. 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями . 3. Скорость движения точки изменяется по закону v=(15t-5t²) м/с. Найдите путь пройденный точкой от начала движения до ее остановки. 4. Вычислите работу, произведенную при сжатии пружины на 0,12 м, если для сжатия ее на 0,01 м нужна сила 20 Н.
Вариант №11 1. Найдите площадь фигуры, ограниченной линиями: а) y=lnx, x=5, y=0. б) 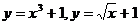2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями y²=8x, y=0, х=1, х=4. 3. Скорость движения точки изменяется по закону v=(3t²-2t+4) м/с. Найдите путь пройденный точкой за 3-ую секунду. 4. Вычислите работу, произведенную при сжатии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна сила 25 Н.	Вариант №12 1. Найдите площадь фигуры, ограниченной линиями: а) y=6x-x², y=0 б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: у=sin2x, y=0, x=0, x=π/2. 3. Скорость падающего в пустоте тела изменяется по формуле V=9,8t. Какой путь пройдет тело за первые 12 с падения? 4. Вычислите работу, произведенную при сжатии пружины на 0,07 м, если для сжатия ее на 0,03 м нужна сила 30 Н.
Вариант №13 1. Найдите площадь фигуры, ограниченной линиями: а) б) 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями: 3. Скорость движения точки изменяется по закону v=(t²+5t-3) м/с. Найдите путь пройденный точкой за 5с от начала движения. 4. Вычислите работу, произведенную при сжатии пружины на 0,1 м, если для сжатия ее на 0,04 м нужна сила 10 Н.	Вариант №14 1. Найдите площадь фигуры, ограниченной линиями: а) б) y=x²+2x+2, y=2-4x-x². 2. Вычислите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у=cosx, y=0, x=0, x=π. 3. Скорость движения точки изменяется по закону v=(4t-8t²) м/с. Найдите путь пройденный точкой от начала движения до ее остановки. 4. Вычислите работу, произведенную при сжатии пружины на 0,06 м, если для сжатия ее на 0,04 м нужна сила 12 Н.

Контрольные вопросы:

1. Геометрический смысл определенного интеграла.

2. Какие прикладные задачи можно решать с помощью определенного интеграла?

3. Запишите формулу для вычисления пройденного пути.

4. Запишите формулу для нахождения работы силы.

5. Запишите формулу для нахождения объема тел вращения.

6. Какие еще знаете примеры применения на практике определенного интеграла?

Практическая работа №18

«Нахождение частных производных, полного дифференциала функций двух переменных»

Цель работы: развить навыки нахождения частных производных функций двух переменны, полного дифференциала, производной неявной функции.

Теоретическая часть

Определение: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие единственное значение переменной z, то переменная z называется функцией двух переменных.

z = f(x, y)

Определение: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие

MM₀<r

также верно и условие.

Записывают: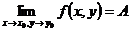

Определение: Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀, у₀), если

(1)

причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом.

Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрывафункции f(x, y).

Пусть в некоторой области задана функция z = f(x, y). Т.к. х и у независимые переменные, то одна из них может изменяться, а другой нет. Рассмотрим случай, когда переменная у не меняется, а х меняется на .Величина D_xz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Если существует предел

То он называется частной производнойфункции z = f(x, y) по х.

Обозначение:

Аналогично определяется частная производная функции по у.

Геометрическим смысломчастной производной является тангенс угла наклона касательной, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности плоскостью у = у₀.

Определение. Для функции f(x, y) выражение Dz = f( x + Dx, y + Dy) – f(x, y) называется полным приращением.

Определение: Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).

(2)

Теорема.Если функция f(x, y) и ее частные производные определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:

. (3)

Т.е. частные производные высших порядков не зависят от порядка дифференцирования.

Производная неявной функции.

Если функция задана неявно, то ее производную можно найти ПО формуле: (4)

Практическая часть

Пример 1. Дана функция z =2х³у⁴-5ln4x+4xу-y. Найдите:

а) Частные производные

б) Частные производные в точке М(-2;3);

в) Полный дифференциал функции;

г) Полный дифференциал функции в точке М;

д) Частные производные второго порядка

Решение.

а)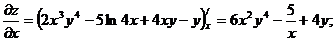

б)

в) Полный дифференциал функции . Подставим в формулу найденные частные производные

г) Подставим в полученное выражение значения частных производных в данной точке:

д)

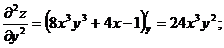
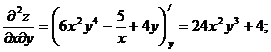
Пример 2. Найти полный дифференциал функции .

Решение.

Пример 3. Найдите производную неявной функции

Решение. 1 способ. Найдем полную производную равенства с учетом того, что у=у(х):

2 способ. Воспользуемся формулой:

В нашем случае

Практические задания:

А) Дана функция z=f(x,y). Найдите:

1. Частные производные

2. Частные производные в т. М(2;-1);

3. Полный дифференциал dz;

4. Частные производные второго порядка функций.

Б) Найдите частные производные и полный дифференциал функций:

В) Найдите производную неявной функции:

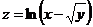Вариант 1 а) б) в)	Вариант 2 а) б) в)
Вариант 3 а) б) в)	Вариант 4 а) б) в)
Вариант 5 а) б) в)	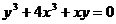Вариант 6 а) б) в)
Вариант 7 а) б) в)	Вариант 8 а) б) в)
Вариант 9 а) б) в)	Вариант 10 а) 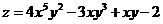б) в)
Вариант 11 а) б) в)	Вариант 12 а) б) в)
Вариант 13 а) б) в)	Вариант 14 а) 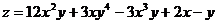б) в)