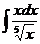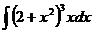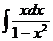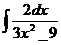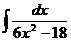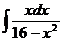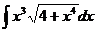Свойства неопределенного интеграла
1) (∫f(x)dx)′ =f(x). 4)  .
.
2) d  . 5)
. 5)  .
.
3)  .
.
Таблица некоторых интегралов
1) 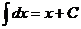 , 10)
, 10) 
2)  ,
, 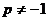 11)
11) 
3)  12)
12) 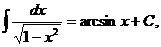
4)  13)
13) 
5)  14)
14) 
6)  15)
15) 
7)  16)
16) 
8)  17)
17) 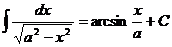
9)  18)
18) 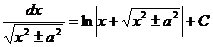
Практическая часть
Непосредственное интегрирование
Этот метод в основном опираться на знания таблиц производных и первообразных.
Пример 1. 
Решение. Применим правило интегрирования (4) и (5), а также табличные интегралы (1) и (2):
 .
.
Пример 2. 
Решение. Применим табличный интерал (14), предворительно преобразав подинтегральное выражение.
 .
.
Замена переменной
Теорема: Если требуется найти интеграл  , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:

Пример 3.  (3x-5)7dx
(3x-5)7dx
Решение. Положим, 3х-5=t, тогда 3dx=dt, dx=1/3dt. Следовательно,
 (3x-5)7dx=
(3x-5)7dx=  t7∙
t7∙  dt=
dt= 
Пример 4. 
Решение.  sin5x dx=
sin5x dx=  sin4x∙sin xdx=
sin4x∙sin xdx=  (1-cos2x)2∙sin xdx.
(1-cos2x)2∙sin xdx.
Положим, cos x=t, тогда -sin xdx=dt, или sin xdx= -dt. Следовательно,
 sin5dx= -
sin5dx= -  (1-t2)2dt= -
(1-t2)2dt= -  (1-2t2+t4)dt= -t+2/3t3-1/5t5+C.
(1-2t2+t4)dt= -t+2/3t3-1/5t5+C.
Пример 5. Найти неопределенный интеграл: 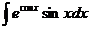 .
.
Решение. 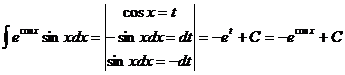 .
.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:  ,
,

или  ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
|
|
|
Пример 6. 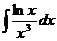 .
.
Решение.
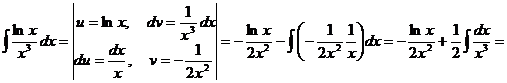
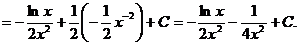
Пример 7.  .
.
Решение. 
 .
.
Как видно, нужно еще раз применить интегрирование по частям:

 .
.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.


Таким образом, интеграл найден вообще без применения таблиц интегралов.
Практическая работа
Интегралы 1-3 найдите непосредственным интегрированием. 
Интегралы 4-6 найдите подстановкой.
Интегралы 7-8 найдите интегрированием по частям.
В-1 

| Вариант 2

|
Вариант 3
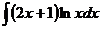
| Вариант 4

|
Вариант 5

| Вариант 6

|
Вариант 7
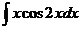
| Вариант 8

|
Вариант 9

| Вариант 10

|
Вариант 11

| Вариант 12
|
Вариант 13

| Вариант 14

|
Контрольные вопросы:
1. Что называется первообразной функции?
2. Что называется неопределенным интегралом?
3. В чем заключается геометрический смысл неопределенного интеграла?
|
|
|
4. Свойства неопределенного интеграла.
5. В чем заключается смысл замены переменной в неопределенном интеграле?
6. В чем заключается смысл интегрирования по частям?
Практическая работа № 15
«Интегрирование рациональных дробей и некоторых иррациональных функций»
Цель работы: формирование умения находить интеграл рациональных дробей, иррациональных функции.
Теоретическая часть
Рациональной дробью называется выражение вида  , где P(x) и Q(x)—многочлены, при этом дробь называется правильной, если степень многочлена P(x) меньше степени многочлена Q(x).
, где P(x) и Q(x)—многочлены, при этом дробь называется правильной, если степень многочлена P(x) меньше степени многочлена Q(x).
Любая правильная дробь можно представить в виде суммы так называемых элементарных дробей.
Отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: Q(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m
Теорема: Если  - правильная рациональная дробь, знаменатель Q(x) которой представлен в виде произведения линейных и квадратичных множителей, то эта дробь может быть разложена на элементарные по следующей схеме:
- правильная рациональная дробь, знаменатель Q(x) которой представлен в виде произведения линейных и квадратичных множителей, то эта дробь может быть разложена на элементарные по следующей схеме:


где A1, A2,…, Aα,…,B1, B2,…,C1, C2,…--некоторые действительные числа, для на нахождения которых применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
|
|
|
Элементарныминазываются дроби следующих четырех типов:
I. 
II. 
III. 
IV. 
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = x -a.
I. 
II. 
III. 
Выделим из трёхчлена в знаменателе полный квадрат
 .
.
Далее следует делать замену: t = x +p/2, откуда х=t-p/2, dx=dt Для удобства обозначим  .
.

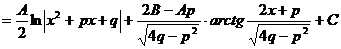 .
.
IV. 

Первый интеграл решается с помощью подстановки t=x2+px+q.

А второй интеграл приводится к виду  , где
, где  ,
,  .
.
Практическая часть.
Рассмотрим применение указанной выше формулы на примерах.
Пример 1. Найдите интегралы: а)  б)
б)  .
.
Решение. а) Интеграл относится к виду I.
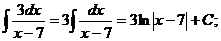
б) 
Пример 2. Найдите интеграл 
Решение. Интеграл относится к виду II.

Пример 3. Найдите интеграл  .
.
Решение. Интеграл относится к виду III.


Пример 4. Найдите интеграл. 
Решение.


Примечание. Если у трехчлена ax2 + bx + c выражение b2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее, ее можно интегрировать указанным выше способом.
|
|
|
Пример.5 Найдите интеграл 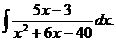
Решение.


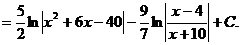
Пример 6. Найдите интеграл 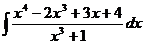 .
.
Решение. Данная подынтегральная дробь неправильная, поэтому, сначала выделим целую часть. Для этого поделим числитель на знаменатель.
__ x4-2x3+3x+4 x3+1
x4+x______ x-2
__ -2x3+2x+4
-2x3-2______
2x+6
Отсюда  .
.
Разложим на множители знаменатель полученной правильной дроби и представим ее в виде суммы простейших:



Приравнивая соответствующие коэффициенты при х2, х и свободные члены левой и правой частях равенства получим систему уравнений:

Решая систему получим: 

 Таким образом,
Таким образом,

Учитывая это, получим:

Примечание. Интеграл  решается аналогично интегралам 4 и 5, решения которых приведены выше.
решается аналогично интегралам 4 и 5, решения которых приведены выше.
Возвращаясь к исходному интегралу, получаем:

Практические задания
Найдите интегралы:
Вариант 1
1.  2.
2.  3.
3.  4.
4. 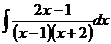 5.
5.  6.
6. 
|   Вариант 2
1. Вариант 2
1.  2.
2.  3.
3.  4.
4.  5.
5. 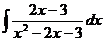 6.
6. 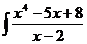
|
Вариант 3
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
| Вариант 4
1. 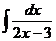 2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
|
Вариант 5
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 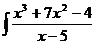
| Вариант 6
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
|
Вариант 7
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
| Вариант 8
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
|
Вариант 9
1.  2.
2. 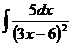 3.
3.  4.
4.  5.
5.  6.
6. 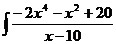
| Вариант 10
1.  2.
2.  3.
3.  4.
4.  5.
5. 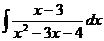 6.
6. 
|
Вариант 11
1.  2.
2.  3.
3.  4.
4.  5.
5. 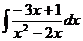 6.
6. 
| Вариант 12
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
|
Вариант 13
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
| Вариант 14
1. 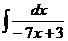 2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
|
Контрольные вопросы:
1. Какая дробь называется правильной?
2. Какие дробиназываютсяэлементарными?
3. В чем состоит суть метода неопределенных коэффициентов?
4. Сформулируйте методы решения интегралов элементарных дробей.
Практическая работа № 13
«Вычисление определенного интеграла».
Цель: сформировать навыки вычисления определенного интеграла.
Теоретическая часть
Пусть функция F(x) является первообразной для функции f(x) в некотором промежутке Х, а числа а и b принадлежат этому промежутку.
Определение. Приращение F(b)-F(a) любой из первообразных функции F(x)+C при изменении аргумента от х=а до х=b называется определенным интегралом от а до b функции f(x) и обозначается  .
.
 – формула Ньютона-Лейбница
– формула Ньютона-Лейбница
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов. Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
Интегрирование по частям.
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла.
Основные свойства определенного интеграла
1) 
2) 
3) Если  то
то 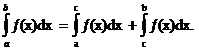
4) 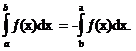
Практическая часть
Пример 1. Вычислить определённый интеграл 
Решение. 
Пример 2. 
Решение. Решим методом подстановки. Пусть  , тогда 2xdx=dt, xdx=1/2dt. Найдём новые пределы интегрирования, подставляя в равенство
, тогда 2xdx=dt, xdx=1/2dt. Найдём новые пределы интегрирования, подставляя в равенство  значения a=-1, b=2.
значения a=-1, b=2.  ,
,  . Следовательно,
. Следовательно,

Пример 3. 
Решение. Интегрируем по частям.


Практические задания
Вычислите интегралы:
1 вариант
1.  2.
2.  3.
3. 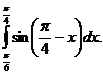 4.
4. 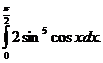 5.
5. 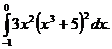 6.
6. 
| 2 вариант
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 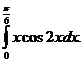
|
3 вариант
1. 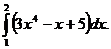 2.
2.  3.
3. 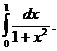 4.
4.  5.
5.  6.
6. 
| 4 вариант
1.  2.
2.  3.
3. 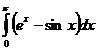 4.
4.  5.
5.  6.
6. 
|
5 вариант
1.  2.
2.  3.
3. 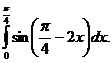 4.
4. 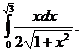 5.
5. 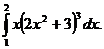 6.
6. 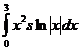
| 6 вариант
1.  2.
2.  3.
3.  4.
4.  5.
5. 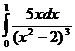 6.
6. 
|
7 вариант
1.  2.
2.  3.
3.  4.
4. 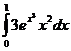 5.
5. 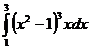 6.
6. 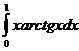
| 8 вариант
1.  2.
2.  3.
3.  4.
4.  5.
5. 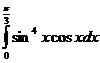 6.
6. 
|
9 вариант
1.  2.
2.  3.
3.  4.
4.  5.
5. 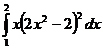 6.
6. 
| 10 вариант
1.  2.
2.  3.
3. 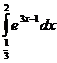 4.
4.  5.
5. 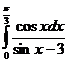 6.
6. 
|
11 вариант
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 
| 12 вариант
1.  2.
2.  3.
3. 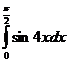 4.
4.  5.
5.  6.
6. 
|
Контрольные вопросы:
1. Что такое определенный интеграл?
2. Зависит ли значение определенного интеграла от выбора первообразной?
3. Чему равен определенный интеграл, если a=b?
4. Сформулируйте свойства определенного интеграла.
Практическая работа №17
«Приложение определенного интеграла»
Цель работы: Научится применять определенный интеграл для нахождения площади плоских фигур, объема тел вращения, пройденного телом пути, работу силы .
Теоретическая часть
Определенный интеграл широко применяется для нахождения различных физических и геометрических величин. Рассмотрим несколько задач.
Дата добавления: 2018-02-18; просмотров: 731; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!