Что называется дифференциалом функции? Чему он равен?
Практическая работа № 11
«Раскрытие неопределенностей. Правило Лопиталя»
Цель работы: Научится раскрывать неопределенности с помощью правила Лопиталя.
Теоретическая часть
(Лопиталь (1661-1704) – французский математик)
К разряду неопределенностей принято относить следующие соотношения:

Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.

Аналогично можно применить правило Лопиталя при раскрытии неопределенности  .
.

Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Практическая часть
Пример 1: Найти предел 
Решение. Как видно, при попытке непосредственного вычисления предела получается неопределенность вида  . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.
 g¢(x) = ex;
g¢(x) = ex;

Пример 2: Найти предел 

Решение. Числитель и знаменатель при х=0 равны нулю, т.е. имеем неопределенность 
|
|
|
 ;
; 


Пример 3: Найти предел 
Решение.  ,
,  .
.

- получили неопределенность. Применяем правило Лопиталя еще раз.
 ,
,  , тогда имеем:
, тогда имеем: 
Пример 3: Найти предел 
Решение. Здесь имеем неопределенность вида 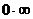 . Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности
. Для решения и таких пределов можно применить правило Лопиталя, предварительно сведя ее к неопределенности  .
.

Пример 3: Найти предел 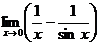
Решение. В данном примере имеется неопределенность вида  . И здесь можно применит правило Лопиталя, сведя ее к виду
. И здесь можно применит правило Лопиталя, сведя ее к виду  .
.



Практические задания
Вариант 1



 





| Вариант 2









|
Вариант 3

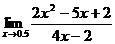



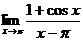
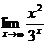


| Вариант 4

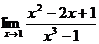







|
Вариант 5





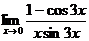



| Вариант 6




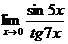




|
Вариант 7
 ; ;
 ; ;
 ; ;

 ; ;
 ; ;
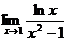 ; ;
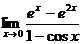 ; ;
 ; ;
| Вариант 8
 . .
 ; ;
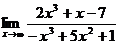 ; ;

 ; ;

 ; ;
 ; ;
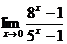 ; ;
|
Вариант 9
 . .
 ; ;
 ; ;
 ; ;
 ; ;
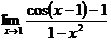 ; ;

 ; ;

|
Вариант 10
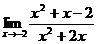 . .


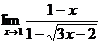



 ; ;
 ; ;
|
Вариант 11
 . .



 ; ;


 ; ;

| Вариант 12
 . .


 ; ;

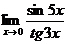

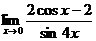 ; ;

|
Вариант 13
 . .
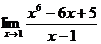

 ; ;
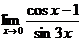 ; ;
 ; ;
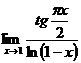 ; ;

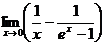 ; ;
| Вариант 14
 . .
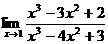


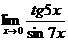 ; ;
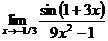 ; ;
 ; ;
 ; ;
 ; ;
|
Контрольные вопросы:
- Перечислите неопределенности в математике.
- Сформулируйте правило Лопиталя.
- В каких случаях можно использовать правило Лопиталя?
Практическая работа №12
«Дифференциал функции. Приближенные вычисления»
|
|
|
Цель работы: Научится находить дифференциал функции. Находить приближенные значения функции с помощью дифференциала».
Теоретическая часть
Пусть функция y = f(x) имеет производную в точке х:
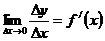
Тогда можно записать: 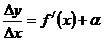 , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно:  .
.
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главная линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx. Для функции х производная равна 1, и потому ее дифференциал равен ∆х, 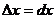 . Поэтому принято вместо
. Поэтому принято вместо  писать dx.. При этом формула дифференциала функции принимает вид:
писать dx.. При этом формула дифференциала функции принимает вид:
dy = f¢(x)dx. (1)
Можно также записать: 


Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv
2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
3) d(Cu) = Cdu
4) 

5)  где
где  .
.
С помощью дифференциала можно найти приближенные значения функции.
Учитывая, что  , приращение функции
, приращение функции  приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
приближённо равно ее дифференциалу, т.е. ∆y»dy, откуда
|
|
|

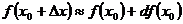 (2)
(2)
Это означает, что приближенное значение функции вблизи точки х0 равно сумме ее значения в этой точке и дифференциала в этой же точке.
Практическая часть.
Пример1. Найдите дифференциал функции: а) 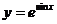 ; б)
; б)  ;
;
в) 
Решение. а) Воспользуемся формулой (1) dy = f¢(x)dx.
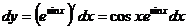
б) 
в) 
Пример2. Вычислить приближённо: а) 2,0025; б)  ; в)
; в)  .
.
Решение. а) Воспользуемся формулой (2):  .
.
Положим  , где х=2,002.
, где х=2,002.
2,002=2+0,002, т.е. 
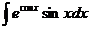


 .
.
Т.о. 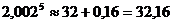 .
.
б) В данном случае  ,
, 
 ;
;

 ;
;

 .
.
в) Рассмотрим функцию  . Полагая х0=450,
. Полагая х0=450,  , имеем:
, имеем:
 ,
,  ,
,  .
.
Т.о.  .
.
Практические задания
Вариант 1
1. Найдите дифференциал функции:
а)  в точке в точке  б)
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х2+3х ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х2+3х ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)  ;
б) sin440. ;
б) sin440.
| Вариант 2
1. Найдите дифференциал функции:
а)  в точке в точке 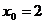 б)
б)  в)
в) 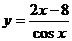 2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=х2-4х ее дифференциалом в точке х=1 при ∆х=0,1.
3. Вычислить приближенно:
а) 2,0035
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=х2-4х ее дифференциалом в точке х=1 при ∆х=0,1.
3. Вычислить приближенно:
а) 2,0035  ;
б) cos310. ;
б) cos310.
|
Вариант 3
1. Найдите дифференциал функции:
а)  в точке в точке  б)
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+3х ее дифференциалом в точке х=1 при ∆х=0,01.
3. Вычислить приближенно:
а)3,9923;
б) tg440.
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+3х ее дифференциалом в точке х=1 при ∆х=0,01.
3. Вычислить приближенно:
а)3,9923;
б) tg440.
| Вариант 4
1. Найдите дифференциал функции:
а)  в точке x=2
б) в точке x=2
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-х2-4х ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-х2-4х ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)  ;
б) arctg1,005. ;
б) arctg1,005.
|
Вариант 5
1. Найдите дифференциал функции:
а)  в точке x=6
б) в точке x=6
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х-х2 ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)4,953;
б) sin310.
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=2х-х2 ее дифференциалом в точке х=3 при ∆х=0,02.
3. Вычислить приближенно:
а)4,953;
б) sin310.
| Вариант 6
1. Найдите дифференциал функции:
а)  в точке x=2
б) в точке x=2
б) 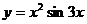 в)
в)  Найдите абсолютную и относительную погрешности при замене приращения функции у=4х+х2 ее дифференциалом в точке х=4 при ∆х=0,01.
2. Вычислить приближенно:
а)
Найдите абсолютную и относительную погрешности при замене приращения функции у=4х+х2 ее дифференциалом в точке х=4 при ∆х=0,01.
2. Вычислить приближенно:
а)  ;
б) arcctg1,030. ;
б) arcctg1,030.
|
Вариант 7
1. Найдите дифференциал функции:
а)  в точке в точке  б)
б)  в)
в) 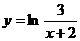 2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,01.
3. Вычислить приближенно:
4. а) 4,0033;
б) ln1,03.
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,01.
3. Вычислить приближенно:
4. а) 4,0033;
б) ln1,03.
| Вариант 8
1. Найдите дифференциал функции:
а)  в точке x=-10
б) в точке x=-10
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х3-x ее дифференциалом в точке х=2 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х3-x ее дифференциалом в точке х=2 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) cos610. ;
б) cos610.
|
Вариант 9
1. Найдите дифференциал функции:
а)  в точке x=4.
б) в точке x=4.
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,04.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+х-1 ее дифференциалом в точке х=3 при ∆х=0,04.
3. Вычислить приближенно:
а)  ;
б) sin620. ;
б) sin620.
| Вариант 10
1. Найдите дифференциал функции:
а) 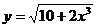 в точке x=3
б) в точке x=3
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=5x-x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=5x-x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)  ;
б) arctg0,9930. ;
б) arctg0,9930.
|
Вариант 11
1. Найдите дифференциал функции:
а)  в точке x=4
б) в точке x=4
б)  2. в)
2. в)   Найдите абсолютную и относительную погрешности при замене приращения функции у=х3+х ее дифференциалом в точке х=3 при ∆х=0,2.
3. Вычислить приближенно:
а) Найдите абсолютную и относительную погрешности при замене приращения функции у=х3+х ее дифференциалом в точке х=3 при ∆х=0,2.
3. Вычислить приближенно:
а)  ;
б) sin470. ;
б) sin470.
| Вариант 12
1. Найдите дифференциал функции:
а)  в точке x=4
б) в точке x=4
б)  в)
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+3х ее дифференциалом в точке х=3 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции у=х2+3х ее дифференциалом в точке х=3 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) ln1,060. ;
б) ln1,060.
|
Вариант 13
1. Найдите дифференциал функции:
а)  в точке в точке  б)
б)  в)
в)   2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x+x3 ее дифференциалом в точке х=4 при ∆х=0,03.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x+x3 ее дифференциалом в точке х=4 при ∆х=0,03.
3. Вычислить приближенно:
а)  ;
б) sin870. ;
б) sin870.
| Вариант 14
1. Найдите дифференциал функции:
а) 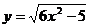 в точке x=3
б) в точке x=3
б)   н
в) н
в)  2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+2x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)
2. Найдите абсолютную и относительную погрешности при замене приращения функции
у=-x3+2x ее дифференциалом в точке х=2 при ∆х=0,1.
3. Вычислить приближенно:
а)  ;
б) arctg0,9920. ;
б) arctg0,9920.
|
Контрольные вопросы
|
|
|
Что называется дифференциалом функции? Чему он равен?
Дата добавления: 2018-02-18; просмотров: 920; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
