Оптимальный режим работы последовательно включенных агрегатов.
Возможная словесная постановка задачи: требуется выбрать режим последовательно соединённых агрегатов так, чтобы при заданной общей производительности и заданных характеристиках конечного продукта затраты на его получение были минимальны.
Введём обозначения:
Xi, Xi + 1 – параметры продукта на входе и выходе i-го агрегата,
Ui – режимные переменные i-го аппарата, являющиеся управляющими воздействиями.
¦0i ( Xi,Ui ) – затраты каждого i-го агрегата на получение продукта.
Тогда критерий оптимальности
I= 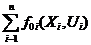 ® min (9.24)
® min (9.24)
На переменные наложены автономные ограничения
Xi Î Vxi Ui Î Vui i = 1,2,…, n
и ограничения, связывающие состав продукта на выходе каждого агрегата с составом на входе и режимными переменными.
X(i+1)υ=f0(Xi, Ui, i), где i=1, 2…n, υ=1, 2…m (9.25)
Где n – количество последовательно включенных агрегатов, m - количество параметров, характеризующих состояния продукта.
Таким образом, в левой части равенств (9. 25) фигурирует n-ая составляющая вектора Xi+1, а в функцию ¦0 входят в общем случае все m составляющих вектора Xi.
Для многих задач оптимизации технологических процессов начальное состояние сырья X1 нельзя считать фиксированным, т.к. оно может изменяться в некоторых, не всегда контролируемых, пределах. В таком случае управляющие переменные Ui можно выбирать либо оптимально в среднем на всём множестве изменения вектора X1, либо они должны быть оптимальны для самого неблагоприятного состава сырья.
|
|
|
Согласование работы периодически
Или циклически действующих аппаратов.
Производительность аппаратов этих типов периодически изменяется. В том случае, когда они работают параллельно на общего потребителя, возникает задача такого выбора сдвигов между моментами начала циклов, при котором отклонение текущей производительности от её среднего значения минимально.
Для формализации задачи введём обозначения: ¦i( t - ti ) – периодическая с периодом T функция, выражающая зависимость производительности i-го аппарата от времени; ti – время сдвига начала цикла i-го аппарата по отношению к началу цикла первого аппарата (t1 = 0).
Оценивая отклонение от средней производительности функционалом
I= 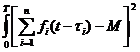 dt ® min (9.26)
dt ® min (9.26)
приходим к задаче выбора вектора t с составляющими ti, оптимизирующего (9.26). Величина M – средняя за период производительность всех N агрегатов равна:
M = 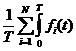 dt (9.27)
dt (9.27)
Рассматривая задачу оптимизации агрегата периодического действия, считали продолжительность цикла Т параметром, подлежащим оптимальному выбору. Если же несколько аппаратов работают параллельно, то продолжительность цикла каждого из них нельзя выбирать независимо. Часто требуется, например, чтобы между остановкой одного агрегата для выгрузки и началом выгрузки следующего агрегата прошло некоторое время tвыг., т.к. загрузку и выгрузку нескольких агрегатов производит одно устройство с ограниченной производительностью. Критерий оптимальности в этом случае представляет собой сумму функционалов вида (9.13), в каждом из которых величины T, q, A и функция ¦0 имеют индекс номера аппарата, то есть
|
|
|
I =  ® min
® min
В задачу кроме ограничений, перечисленных для критерия (9.13), следует добавить условие
ê( ti + Ti + qi ) – ( tn + Tn + qn ) ê ³ tвыг n ¹ i
где ti и tn – моменты начала циклов для i-го и n-го аппаратов.
Литература.
1.Цирлин А.М. Оптимальное управление технологическими процессами: Учебное пособие для вузов - М.: Энергоатомиздат, 1986 – 400 с.
2.Автоматическое управление в химической промышленности:
Учебник для вузов. Под ред. Е.Г. Дудникова. - М.: Химия, 1987 – 368 с.
|
|
|
3.Теория автоматического управления. Часть II. Под ред. А.А. Воронова - М.: Высшая школа, 1977 – 288 с.
Дата добавления: 2018-02-15; просмотров: 501; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
