Определение условного максимума функционала

С ограничениями типа дифференциальных уравнений.

Принцип максимума Понтрягина.

(7.11)

i = 1, 2, …, n. (7.12)

Для решения задачи (7.11), (7.12) используется необходимые условия оптимальности, известные как принцип максимума Понтрягина. Составляем функционал Понтрягина:

(7.13)

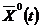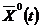Если и решение задачи (7.11), (7.12), то найдется такой вектор , что при и функция Н достигает максимум по

(7.14)

Составляющие вектора являются решением системы дифференциальных уравнений.

(7.15)

с граничным условием , (7.16)

если не заданы составляющие при t=T. Если условия заданы в общем виде

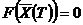, (7.17)

то (7.18)

Последовательность решения задачи (7.11) (7.12)

1) Составляем функционал Н в соответствии с (7.13) и из условия (7.14) определяем

2) Решаем систему уравнений (7.15) для переменных с граничными условиями (7.16) или (7.18).

3) Решаем систему дифференциальных уравнений (7.12) совместное решение позволяет найти .

8. Оптимальное управление технологическими процессами.

Формирование критериев оптимальности.

Любой технологический процесс характеризуется рядом показателей - таких как производительность G, вектор К, определяющий качество выходного продукта, показатель надежности Р, капиталовложения М, затраты на обслуживание . Как уже указывалось выше (см. раздел 1.4) возможны два подхода к формулированию оптимизационных задач. При первом походе в качестве критерия оптимальности выбирается один из показателей функционирования процесса, наиболее важный с точки зрения постановщика задачи, а остальные учитываются при формировании ограничений.

Однако часто возникает желание оптимизировать одновременно несколько показателей функционирования. При этом можно пойти по пути формирования сводного критерия оптимальности, так или иначе включающего в себя показатели, подлежащие оптимизации (частные критерии) или обойтись без него.

Возможные способы формулировки задачи оптимизации с несколькими частными критериями рассмотрены в этом разделе.

Способы формирования сводного критерия оптимальности.

Обозначим через I_υ υ-ый показатель функционирования процесса и будем для простоты считать, что в результате оптимизации желательно каждый из m таких показателей (частных критериев) увеличить. Если некоторые из показателей, например капиталовложения М, нужно уменьшить, то соответствующий им частный критерий I_υ, примем равным -М. Через обозначим параметры процесса и системы управления, подлежащие оптимальному выбору (переменные управления), и будем первоначально считать задачу полностью детерминированной, полагая, что значение каждого из частных критериев становится известным при заданных . Совокупность ограничений, накладываемых на оптимизируемые параметры управления составит область допустимых значений варьируемых переменных.

Для пояснения способов формирования сводного критерия ограничимся случаем с двумя переменными U₁ и U₂, подлежащими выбору и двумя частными критериями I₁ и I₂, геометрическая интерпретация которого представлена на рис. 8.1.

Рис.8.1

U₁

Каждой точке

на плоскости управлений

соответствует точка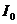

на плоскости критериев I.

Аналогично отображая каждую точку границы области допустимых значений управлений V, получаем на плоскости критериев область допустимых значений критериев I, включающую в себя все значения частных критериев I₁ и I₂, которые могут быть получены, при допустимых значениях управлений U₁ и U₂.

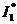Очевидно, что оптимальное решение по одному критерию приводит в точку и не совпадает с оптимальным решением по другому критерию (точка ). Чтобы найти оптимальное решение , можно пойти по пути формирования из частных критериев I_υ сводного критерия . Рассмотрим несколько способов получения сводного критерия.

Дата добавления: 2018-02-15; просмотров: 523; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒

Мы поможем в написании ваших работ!