Определение максимума функционала.
(Вариационная задача оптимизации).
Пример постановки вариационной задачи.
Как указывалось выше (см. раздел 1.3), функционалом называется функция, аргументом которой является другая функция. Функционал обычно формируется в виде интеграла, определенного в некоторых пределах, и решить вариационную задачу, значит найти выражение функции, которая обеспечит максимум этого интеграла.
Рассмотрим постановку и решение оптимизационной задачи на простейшем примере.
Пример. Определить уравнение, описывающее функцию, график которой проходит через две заданных точки и имеют между ними наименьшую длину.
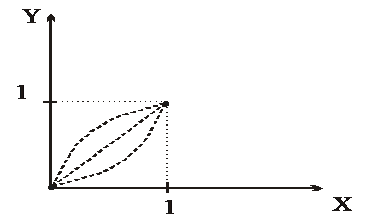
.
Рис. 7.1
Пусть одна из точек находится в начале координат 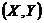 , а другая в точке с координатами
, а другая в точке с координатами 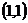 .
. 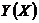 - функция, проходящая через две точки (рис. 7.1),
- функция, проходящая через две точки (рис. 7.1),  - элементарный участок функции
- элементарный участок функции 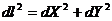
|
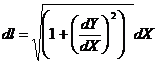
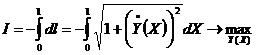
Знак «минус» появился перед интегралом при переформулировании задачи нахождения минимума на задачу нахождения максимума.
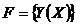 - функционал,
- функционал, 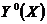 - экстремаль (максималь или минималь) - искомое уравнение функции, обеспечивающее экстремум функционала.
- экстремаль (максималь или минималь) - искомое уравнение функции, обеспечивающее экстремум функционала.
Определение безусловного максимума функционала.
(Классическая вариационная задача), (задача Эйлера).
Постановка задачи:
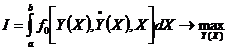 (7.1)
(7.1)
Необходимое условие оптимальности определяется уравнением Эйлера.
|
|
|
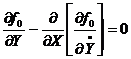 (7.2)
(7.2)
Из выражения (7.2.) вытекают два частных случая:
Если  явно не зависит от
явно не зависит от 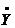 , то
, то  (7.3)
(7.3)
Если  явно не зависит от
явно не зависит от 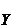 , то
, то 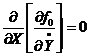 , (7.4)
, (7.4)
откуда следует  (7.5)
(7.5)
Условие (7.2) дополняется следующим условием Лежандра
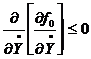 (7.6)
(7.6)
Если выполняются условия (7.2) и (7.6), то 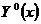 - максималь.
- максималь.
Рассмотрим решение примера, условия которого сформулированы в разделе 7.1.
Так как подынтегральная функция 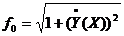 не зависит явно от Y, то используем условие оптимальности Эйлера (7.5). Внеся минус под знак интеграла, получим.
не зависит явно от Y, то используем условие оптимальности Эйлера (7.5). Внеся минус под знак интеграла, получим.
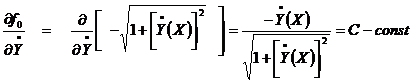 , откуда получаем
, откуда получаем

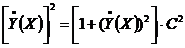 ,
,
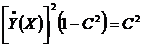 , следовательно,
, следовательно, 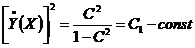 ;
;
Отсюда следует, что  .
.
Интегрируя, находим 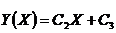 , где С3 – постоянная интегрирования.
, где С3 – постоянная интегрирования.
Для нахождения значений С2 и С3 используем начальные условия задачи, т.е. координаты заданных точек: Y = 0 при X = 0, следовательно С3 = 0; Y = 1 при X = 1, следовательно С2 = 1.
Окончательно получаем 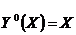
Проверка условия Лежандра. Учитывая, что 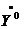 (X)=1, имеем:
(X)=1, имеем:
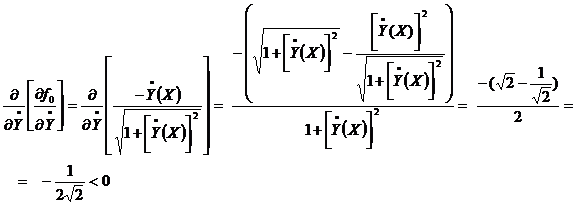
т.е. 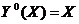 - максималь, что и требовалось доказать.
- максималь, что и требовалось доказать.
|
|
|
Определение условного максимума функционала
(неклассическое вариационное исчисление)
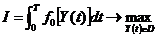 (7.7)
(7.7)
 (7.8)
(7.8)
Для решения задачи (7.7), (7.8) используется метод, аналогичный методу неопределенных множителей Лагранжа. Составляется функционал Лагранжа.
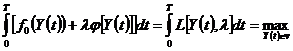
Доказано, что если функция 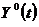 является решением задачи (7.7), (7.8), то найдется такое значение
является решением задачи (7.7), (7.8), то найдется такое значение  , при котором
, при котором 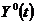 обеспечивает безусловный максимум функционала Лагранжа.
обеспечивает безусловный максимум функционала Лагранжа.
Таким образом, необходимым условием оптимальности для задачи (7.7), (7.8) является условие максимума функции L по 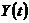 , .т.е.
, .т.е.
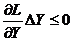 (7.9)
(7.9)
В частности, если автономные ограничения отсутствуют, то условие (7.9) сводится к
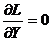 (7.10)
(7.10)
Пример.
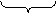
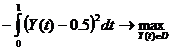
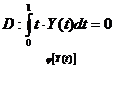
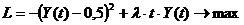
Так как автономные ограничения отсутствуют, применяем необходимые условия оптимальности в форме (7.10)
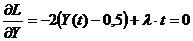 , откуда получаем
, откуда получаем 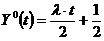 Для нахождения λ подставляем Y0(t) в интеграл ограничений.
Для нахождения λ подставляем Y0(t) в интеграл ограничений.
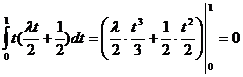 ,
,
Подставляя пределы интегрирования, получаем 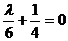 , откуда
, откуда 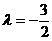
|
|
|
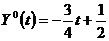
Задача решена.
Найдем максимум критерия оптимальности.
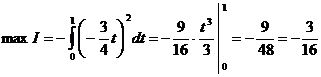
Дата добавления: 2018-02-15; просмотров: 951; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
