Численные методы решения задачи. При решении задача (4.1.) – (4.4) должна быть преобразована в задачу безусловной оптимизации, к которой можно применить различные методы многомерного поиска:
При решении задача (4.1.) – (4.4) должна быть преобразована в задачу безусловной оптимизации, к которой можно применить различные методы многомерного поиска: покоординатного спуска, градиента, симплекс и т.д.
Метод штрафных функций
Перевод задачи (4.1.) – (4.4.) к задаче безусловной оптимизации осуществляется введением в целевую функцию дополнительных слагаемых, которые «штрафуют» за нарушение любого из условий (4.3.) или (4.4.), т.е. осуществляется переход к новой целевой функции вида:
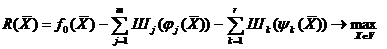(4.25)
Функция Ш выбирается так, чтобы она была равна нулю, если соответствующее ей ограничение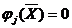 
или 
, выполняется и много больше нуля, если не выполняется.
Исходя из этого, обычно выбирают:
(4.26)
(4.27)
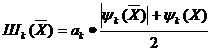(4.28)
(4.29)
Таким образом, при поиске безусловного максимума 
значение этой функции будет возрастать до тех пор, пока при расчетах используются значения варьируемых переменных 
, обеспечивающие выполнение всех ограничений типа связи и функциональных ограничений, накладываемых на исходную целевую функцию 
, а как только значения выйдут из области допустимых значений D, значение функции резко уменьшиться, т.е. поиск безусловного максимума функции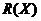 
всегда будет проводиться в области 
, т.е. соответствовать поиску условного максимума целевой функции 
.
|
|
|
Для обеспечения выполнения условия (4.27) и (4.29) необходимо выбирать α = const >>1. Решение задачи (4.25) точно совпадает с решением исходной задачи (4. 1) – (4.4.) только при α → ∞. Практическая точность зависит от величины коэффициентов α и увеличивается с их ростом. Однако введение штрафных функций вызывает деформацию линий равного уровня целевой функции. На ее поверхности образуются гребни и овраги, что затрудняет численную процедуру поиска (см. раздел 3.3.2.1.).
Крутизна гребней и оврагов возрастает с увеличением α, поэтому целесообразно решение искать в несколько этапов.
Вначале, принимают α (0) - малым и находят решение 
(α(0)), которое значительно отличается от истинного. Полученный результат принимается за начальное приближение для следующего этапа расчета при α(1) > α(0), в результате получается значение (α(1)), более близкое к истинному и т.д. Таким образом, поиск на каждом этапе происходит в окрестности решения, где овражность сказывается меньше.
Расчет заканчивается, когда 
где N – число этапов расчета.,
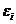- заданная допустимая погрешность расчета переменной Хi,
|
|
|
n – количество варьируемых переменных целевой функции.
Оптимизация многостадийных процессов
Постановка задачи на примере и ее формализация.
Рассмотрим технологическую схему получения ректифицированного спирта, представленную на рис. 5.1.
Рис 5.1.
С0, С1, С2,С3 - концентрации спирта;
G1, G2, G3 - расходы пара;
C1= F1 (C0, G1); C2= F2 (C1,G2); C3= F3 (C2,G3);
где F1, F2, F3 функции, связывающие выход и вход на каждой стадии ректификации.
Необходимо минимизировать расход пара, т.е. найти такие
G10,G20,G30, при которых
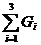→ min
Учитывая, что argmax f0(X) = argmin (-f0(X)), (см. раздел 1.4.), получаем оптимизационную задачу для многостадийного процесса.
- → 
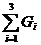Gi* ≤ Gi ≤ Gi * i = 1, 2, 3
D= Ci - Fi (C i-1, Gi) = 0
C3 ≥ Cзад
Формализуя данную задачу для процесса из n стадий, получаем структурную схему, представленную на рис. 5.2. , для каждого элемента которой выполняется условие Xi = fi(Xi-1, Ui) и формируется целевая функция f0i (Xi, Ui) (в примере Gi).
Рис. 5.2
Где,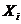 
- переменные состояния ( в примере Ci )
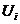- переменные управления (в примере Gi)
Для всего процесса получаем:
|
|
|
I = 
( 
) → 
, (5.1.)
где n – количество стадий (этапов) процессов.
|
Последовательность управлений U1, U2…Un (см. рис. 5.2) называется стратегией управления.
Оптимизация многостадийных процессов сводится к отысканию оптимальной стратегии управления, которая обеспечит перевод процесса из заданного начального состояния X0 в заданное конечное состояние Xn с минимальными затратами на управление.
5.2. Решение задачи методом неопределенных множителей Лагранжа.
Оптимизационная задача (5.1.) – (5.4.) представляет собой задачу определения условного max с автономными ограничениями (5.3), (5.4) и ограничениями типа связи (5.2). Как известно (см. раздел 4.2.1.) такая задача может быть решена методом неопределенных множителей Лагранжа:
(Xi, Ui)+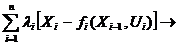 
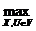
Необходимые условия оптимальности
(5.6.)
D=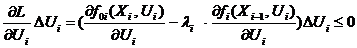 
(5.7.)
= Xi - fi (X i-1 , Ui) = 0 (5.8.)
Поясним вывод выражения (5.6.). Например, для n = 2 имеем:
L = f01 (X1U1) + f02(X2 U2) + λ1 (X1 - f1 (X0U1)) + λ2 (X2 – f2 (X1 U2))
Произведя замену для случая 
стадий 
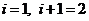, получаем выражение (5.6), которое является рекуррентной формулой для расчета λ i. через λi+1.
|
|
|
(5.9.)
Для его использования задается граничное условие. Очевидно, что после окончания процесса
λ n+1 = 0 (5.10.)
Пример:
Из условия примера следует:
Вычисляем значения частных производных, содержащихся в правой части выражения (5.9.).
для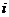 
=1, 2, 3
Составляем функцию Лагранжа аналогично (5.5.):
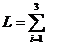(Xi, Ui)+ 
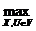
Из выражения (5.10) для случая n=3 имеем:
λn+1 = λ4 = 0
По выражению (5.9) вычисляем λi (i=1,2,3), используя значения частных производных, вычисленные выше
λ2 = λ3 ּ 1 - 1 = (-1) ּ 1 - 1 = - 2
λ1 = (- 2) ּ 1 – 1 = - 3
Проверяем выполняемость условия (5.7)
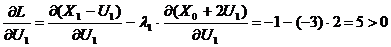
Так как производные 
, (i=1,2, 3) больше нуля, то необходимое условие оптимальности (5.7) может быть выполнено только при ∆Ui < 0, т.е. при верхнем граничном значении управления (см. раздел 1.4.), следовательно, U10=U20=U30=1.
Зная оптимальные значения переменных управления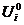 
, (i=1,2, 3), рассчитываем оптимальные значения переменных состояния Xi0 по уравнению связи (5.8).
X10 = X0 + 2U1 = 1 + 2 · 1 = 3
X20 = 3 + 2 · 1 = 5
X30 = 5 + 2 · 1 = 7
Вычисляем максимальное значение критерия оптимальности
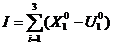= (3 – 1) + (5 – 1) + (7 – 1) = 12
Задача решена.
Дата добавления: 2018-02-15; просмотров: 868; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!