Численные методы первого порядка (градиентные)

3.3.3.1. Постановка задачи.

Понятие градиента и его геометрическая интерпретация.

,        V:  , где 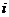 = 1,2…n.

Градиентом функции  называется вектор в пространстве варьируемых переменных , направление которого в данной точке соответствует наискорейшему возрастанию функции.

 Построение вектора градиента производится по его проекциям на оси координат, которые равны частным производным целевой функции по соответствующим переменным.

, в  max

В двумерном случае в любой точке на плоскости переменных  градиент направлен перпендикулярно касательной, проведённой к линии равного уровня в данной точке (рис. 3.8).

                                        

                                  Рис. 3.8

Метод градиента.

Метод градиента – это пошаговая процедура поиска max целевой функции , в которой каждый шаг поиска выполняется в направлении градиента, исходящего из предыдущей точки. Координата очередной точки после К-го шага поиска определяется по формуле:

    (3.8),

где -const, определяющая величину К-го шага.

Выбор  производится, исходя из компромисса между скоростью поиска (растет при больших ) и точностью (растёт при малых ). Правильным считается такой выбор , при котором угол между направлениями вектора градиента в двух последовательных точках находится в пределах от 15⁰ до 30⁰. О величине угла  удобно судить по cos этого угла, который вычисляют как отношение скалярного произведения градиентов  и  к произведению их модулей.

 

       (3.9)

 

При 15⁰ ≤ α ≤ 30⁰               0,85 ≤ cos α ≤ 0,95                         (3.10)

Расчет производится следующим образом:

 

1.Выбирается начальная точка (0) c координатами X_i(0), i=1,2…n.

2. Производится расчет проекций вектора градиента в начальной точке .

3.Выбирается γ и по формуле (3.8) определяются координаты следующей точки (1).

4.Производится расчет проекций вектора градиента в точке (1).

5.По формуле (3.9) определяется cos α.

6.Если условие (3.10) выполняется, то проводится расчет по пунктам 3-5 для точек (1) и (2) и т. д. Если (3.10) не выполняется, то величина γ корректируется и повторяется расчет по пунктам 3-5 для точек (0) и (1).

Остановка алгоритма производится при равенстве с заданной точностью нулю вектора градиента  или  или задается количество шагов N и за решение принимается последняя полученная точка (N).

Как видно из изложенного алгоритма, расчет достаточно громоздкий, причем заранее неизвестно, сколько раз придется рассчитывать один и тот же шаг. Мало того, что не определены критерии первоначального выбора коэффициента шага , но и нет гарантии, что повторный расчет будет удачным и не придется пересчитывать тот же самый шаг еще несколько раз. Действительно, после первого неудачного расчета шага мы получаем информацию только о том нужно ли уменьшить шаг (в случае , т.е. ) или увеличить ( , т.е. ), но насколько надо изменить шаг, чтобы второй расчет оказался стопроцентно удачным, неизвестно. Этих недостатков лишен метод крутого восхождения.

 

Метод крутого восхождения.

Метод крутого восхождения отличается от метода градиента правилом определения коэффициента шага γ.

    Он должен быть таким, чтобы f₀ достигала max по направлению градиента при данном значении γ, т.е.

=arg max                                                        (3.12).

где k= 1,2,3…- номер шага поиска

Поясним это требование на примере рис.3.8. Помня о том, что чем ближе сомкнуты линии равного уровня к максимуму тем большему значению целевой функции они соответствуют, можно сделать вывод, что целевая функция при движению по градиенту из точки A, будет возрастать примерно до точки С, а при дальнейшем движении начнет уменьшаться.

Таким образом в методе крутого восхождения ставится задача расчета такой величины коэффициента шага , чтобы за один шаг попасть из точки А в точку С.

Пример:

Для f₀( ) = -X₁² + X₁ X₂ - X₂² + X₁ выполнить один шаг поиска максимума из начальной точки (0) с координатами X₁(0)=5, X₂(0)=2, методом градиента и  методом крутого восхождения

I. Метод градиента:

1. Рассчитываем проекции вектора градиента в начальной точке

а₁(0) = = (-2X₁+X₂+1) = -2 • 5 + 2 + 1 = -7

а₂(0) = = (X₁-2X₂) = 5 – 2 • 2 = 1

2. Выбираем для первого шага γ₁=0,3

3. Рассчитываем координаты точки (1) после первого шага по выражению (3.8)

X₁(1) = X₁(0) + γ₁ a₁(0) = 5 + 0,3 • (-7) = 2,9

X₂(1) = X₂(0) + γ₁ a₂ (0) = 2 + 0,3 • 1 = 2,3.

4. Определяем проекции вектора градиента в точке (1)

а₁(1) = = -2 • 2,9 + 2,3 + 1 = -2,5

а₂(1) = = 2,9 – 2 • 2,3 = -1,7

 

5. Вычисляем модули градиента в точках (1) и (0)

6. Определяем  cos α

сos α= =

Условие (3.10) не выполняется, необходимо уменьшить шаг. Выбираем γ₁=0,2 и пересчитываем.

Поскольку проекции вектора градиента а₁(0)=-7 и а₂(0)=1 в исходной точке остались теми же самыми, сразу определяем координаты первой точки, т. е. повторяем пункт 3 расчета при значении γ₁=0,2.

(1)=5+0,2*(-7)=3,6

(1)=2+0,2*1=2,2

Определяем проекции вектора градиента в точке (1), аналогично пункту 4

а₁(1)=-2*3,6+2,2+2=-4

а₂(1)=3,6-2*2,2=-0,8

Вычисляем модуль градиента в точке (1) и пересчитываем  значение cos α, аналогично пунктам 5 и 6.

сos α=

Условие (3.10) выполнено, следовательно, для первого шага выбираем коэффициент γ₁=0,2.

Рассчитываем значения целевой функции в нулевой и первой точках.

Значение целевой функции после первого шага возросло, следовательно, расчет сделан правильно.

II. Метод крутого восхождения.

По выражению (3.8) определяем координаты первой точки (1) как функции от коэффициента шага γ₁, используя значения проекций вектора градиента, рассчитанных выше.

(1)= (0)+γ₁a₁(0)=5+ γ₁*(-7)=5-7 γ₁

(1)= (0)+γ₁a₂(0)=2+ γ₁*1=2+ γ₁

Подставляем полученные выражения (1) , (1) в . Необходимо, чтобы полученное выражение достигало max по γ₁ .

(γ₁)=-(5-7γ₁)²+(5-7γ₁)(2+γ₁)-(2+γ₁)²+(5-7γ₁)→max

Для этого производная  должна быть равна нулю.

=-2(5-7 γ₁)*(-7)+(-7)(2+ γ₁)+(5-7 γ₁)-2(2+ γ₁)+(-7)=0

Отсюда γ₁=0,44.

По выражению (3.8) определяем координаты первой точки (1)

(1)=5-0,44*7=1,93

(1)=2+0,44*1=2,44

Вычисляем значение целевой функции в точке (1) и сравниваем его со значением в точке (0), вычисленным ранее.

 >

Сравнивая значения целевой функции после первого шага вычислений двумя рассмотренными методами

а также объем вычислений на этом шаге, приходим к выводу о большей эффективности метода крутого восхождения.

 

4. Определение условного максимума  функции нескольких переменных.

Методы нелинейного программирования

---

Дата добавления: 2018-02-15; просмотров: 1125; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!