Постановка задачи. Методы решения оптимизационных задач.
В данном случае в критерии оптимальности присутствует только одна варьируемая переменная. На нее могут быть наложены только автономные ограничения и постановка задачи принимает вид:
 (2.1)
(2.1)
 (2.2)
(2.2)
В соответствии с теоремой Вейерштрассе всякая функция  , непрерывная на замкнутом и ограниченном множестве (
, непрерывная на замкнутом и ограниченном множестве (  ), достигает на нем своего наибольшего и наименьшего значения. Функция
), достигает на нем своего наибольшего и наименьшего значения. Функция  выпукла на
выпукла на  , если она имеет на этом множестве единственный максимум. Выпуклая функция обладает тем свойством, что, если через две любые принадлежащие ей точки провести прямую (с координатами
, если она имеет на этом множестве единственный максимум. Выпуклая функция обладает тем свойством, что, если через две любые принадлежащие ей точки провести прямую (с координатами  и
и 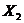 ), то любая промежуточная точка этой прямой не будет превышать значение функции при том же Х (рис.2.1). Для выпуклой функции справедливо выражение:
), то любая промежуточная точка этой прямой не будет превышать значение функции при том же Х (рис.2.1). Для выпуклой функции справедливо выражение:
 , где
, где 
Если функция не выпукла (неунимодальна), то она будет иметь несколько точек максимума, причем значение функции в этих точках будет различным (рис. 2.2)
В этом случае точка, соответствующая наибольшему значению функции (точка  на рисунке) называется точкой глобального максимума, а остальные точки (
на рисунке) называется точкой глобального максимума, а остальные точки (  ,
, 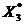 ,
,  ,
,  ) – локальными максимумами функции.
) – локальными максимумами функции.



Рис.2.1
Все методы решения оптимизационных задач, в том числе методы определения максимума функции одной переменной делятся на:
1. Аналитические, основанные на необходимых или достаточных условиях оптимальности, причем достаточные условия применяются только в случае сложноорганизованных областей допустимых значений D.
|
|
|
2. Численные, которые представляют собой вычислительную процедуру, обеспечивающую последовательное уточнение решения от некоторого начального приближения до максимума с заданной допустимой погрешностью.
Аналитический метод решения задачи. Условия максимума функции одной переменной.
Пусть  - непрерывная и дважды дифференцируемая функция при
- непрерывная и дважды дифференцируемая функция при  и X0 - точка предполагаемого маусимума функции. Для того, чтобы при X0 функция достигала max необходимо, чтобы при любом другом Х, сколь угодно близком к X0, т.е.
и X0 - точка предполагаемого маусимума функции. Для того, чтобы при X0 функция достигала max необходимо, чтобы при любом другом Х, сколь угодно близком к X0, т.е.  , выполнялось соотношение
, выполнялось соотношение  (2.3)
(2.3)
Разложим  в ряд Тейлора в окрестности точки X0
в ряд Тейлора в окрестности точки X0
 (2.4)
(2.4)
При небольших DХ, членами, содержащими приращения в степени больше единицы можно пренебречь и тогда из (2.4) следует:
 . (2.5)
. (2.5)
Подставляя (2.5) в (2.3) окончательно получаем необходимое условие максимума функции одной переменной:
 (2.6)
(2.6)
При использовании этого условия могут возникнуть два варианта:
1.  - внутренняя точка интервала допустимых значений (рис. 2.3). В этом случае знак DХ не определен и для выполнения условия (2.6) необходимо
- внутренняя точка интервала допустимых значений (рис. 2.3). В этом случае знак DХ не определен и для выполнения условия (2.6) необходимо
|
|
|
 (2.7)
(2.7)
При этом знак разности (2.3) определяется знаком первого отброшенного члена ряда Тейлора, т.е. знаком  . Поэтому необходимое условие max (2.7) дополняется условием
. Поэтому необходимое условие max (2.7) дополняется условием
 (2.8)
(2.8)
2.  - граничная точка интервала
- граничная точка интервала  . В этом случае знак DХ определен (рис. 2.4) и для расчетов будем использовать выражение (2.6).
. В этом случае знак DХ определен (рис. 2.4) и для расчетов будем использовать выражение (2.6).



Рис.2.3. Х* Х* Х
Рис. 2.4.
Сформулируем правила применения необходимых условий максимума функции одной переменной.
1. Определяют все корни уравнения (2.7), являющиеся внутренними точками отрезка  и для каждого из них проверяют условие (2.8). Удовлетворяющие ему корни являются точками локальных максимумов целевой функции.
и для каждого из них проверяют условие (2.8). Удовлетворяющие ему корни являются точками локальных максимумов целевой функции.
2. Рассчитывают значение функции  в этих точках и сравнив их между собой определяют глобальный максимум.
в этих точках и сравнив их между собой определяют глобальный максимум.
3. Если среди корней уравнения (2.7), нет значений, принадлежащих множеству допустимых решений, необходимо проверить граничные точки  и
и  с использованием условия (2.6).
с использованием условия (2.6).
|
|
|
Пример. Определить максимум функции  при
при
а)  , б)
, б)  , в)
, в)  ;
;



а) X0 = 0.6, внутренняя точка отрезка  , следовательно, знак ΔX не определен и необходимо проверить выполнение условия (2.8).
, следовательно, знак ΔX не определен и необходимо проверить выполнение условия (2.8).
 < 0
< 0
Условие (2.8) выполняется.
Ответ: 
б)  , проверим
, проверим 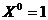 - нижняя граница отрезка
- нижняя граница отрезка  , следовательно, DХ > 0.
, следовательно, DХ > 0.
Проверяем выполнение условия (2.6).
 < 0.
< 0.
Условие (2.6)  выполняется, т.е.
выполняется, т.е.  .
.
в)  . Проверим Х = 0.5 – верхняя граница отрезка
. Проверим Х = 0.5 – верхняя граница отрезка  , следовательно, DХ < 0.
, следовательно, DХ < 0.
Проверяем выполнение условия (2.6):  > 0
> 0
Условие (2.6) выполняется, т.е. 
Дата добавления: 2018-02-15; просмотров: 562; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
