Пример 1. Выбор оптимального расположения узла при прокладке трасс.

⇐ ПредыдущаяСтр 2 из 21Следующая ⇒

Словесная постановка. Задано расположение нескольких потребителей сырья. Требуется так выбрать расположение промежуточной емкости, из которой снабжают всех потребителей, чтобы суммарная длина трубопроводов была минимальной, (рис. 1.1).

Рис. 1.1

Введение обозначений для переменных. Обозначим через координаты емкости на плоскости, а через 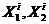- координаты i-того потребителя. Расстояние от емкости до i-го потребителя выразим как .

Критерий оптимальности ® min.

Множество допустимых решений D: в данном случае все действительные значения переменных .

Заметим, что здесь и в дальнейшем искомое решение, т.е. значения варьируемых переменных, претендующие на максимум, будем обозначать через 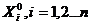, где n - количество варьируемых переменных в данной задаче.

₁

Рис. 1.1 Рис. 1.2

Пример 2. Выбор оптимальных размеров цилиндрической емкости.

Словесная постановка. Выбрать длину образующей и диаметр днища цилиндра, таким образом, чтобы при заданном объеме, общая длина сварных швов оказалась минимальной (рис.1.2).

Обозначения для переменных. l и d – длина образующей и диаметр цилиндра, V_зад –заданный объем цилиндра.

Критерий оптимальности: общая длинасварных швов

® min.

Множество допустимых решений:

D =

Замена переменных:

X₁=d, X₂=l,

(X)=2 π X₁+X₂→min,

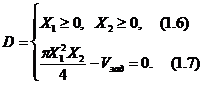
Пример 3. Распределение нагрузок между параллельно включенными агрегатами.

Рис. 1.3

Словесная постановка.Заданную нагрузку по сырью, т. е. имеющийся в наличии запас сырья, распределить между параллельно включенными агрегатами так, чтобы общая производительность была максимальной.

рис1.3

Обозначения для переменных.

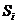- потребление сырья i-м агрегатом,

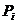- его производительность. Зависимость производительности аппарата от нагрузки называют нагрузочной характеристикой. Типичный вид нагрузочной характеристики представлен на рис. 1.3.

Критерий оптимальности – суммарная производительность: 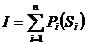® max,

где n-количество агрегатов.

Множество допустимых решений: задание максимально допустимой нагрузки для каждого агрегата S_i^* и суммарной нагрузки по сырью, т.е. количества распределяемого сырья S_зад, приводят к ограничениям:

D =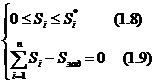

Классификация оптимизационных задач.

Приведем классификацию оптимизационных задач по характеру искомого решения (рис. 1.4). Это задачи о безусловном максимуме функции одной и нескольких переменных, решением их является вектор , где X₁, X₂, …,Х_n – значения варьируемыхпеременных, причем на эти переменные не наложено никаких ограничений, либо наложены автономные ограничения .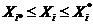

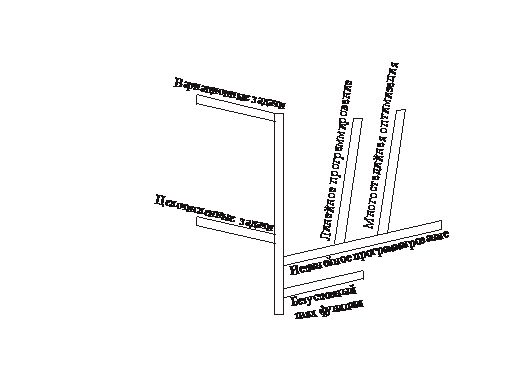
Рис. 1.4

Задачи об условном максимуме функций называют задачами математического программирования, в общем случае нелинейного программирования. Их решением также является вектор , причем в этом случае на варьируемые переменные X₁, X₂, …,X_n накладываются ограничения типа связи в виде равенств j_j( ) = 0, j = 1,2,...,m и (или) функциональные ограничения в виде неравенств y_к( )£ 0, k=1,2,…,r, где j_j( ) и y_к( ) – функции, которые определяются из условий решаемой оптимизационной задачи. Автономные же ограничения могут как присутствовать, так и отсутствовать.

Важным частным случаем такой задачи является задача линейного программирования, в которой критерий оптимальности и ограничения линейно зависят от варьируемых переменных. Суть задачи оптимизации многостадийных процессов состоит в определении оптимальной стратегии управления, т.е. оптимальной последовательности управляющих воздействий на каждом этапе (стадии) процесса.

Если значения искомых переменных могут принимать лишь целочисленные значения, то задачу называют целочисленной или комбинаторной. Параметром такой задачи может служить задача оптимального планирования грузоперевозок, в которой нужно распределить имеющиеся количество автотранспорта по различным маршрутам.

Наконец, если решением задачи является функция, то задачу называют вариационной или задачей об оптимуме функционала.

Критерий оптимальности.

В задачах, где переменными являются составляющие некоторого вектора, критерий оптимальности представляет собой функцию нескольких переменных, а в задачах, где искомым решением является функция, критерий оптимальности является функционалом. Функционал представляет собой функцию, аргументом которой является другая функция от независимой переменной, т.е. 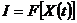. Обычно в вариационных задачах функционал выражается в виде определенного интеграла от функции, аргументом которой является время. Целью решения вариационной задачи является нахождение такой подынтегральной конкретной функции, которая обеспечивает оптимум (максимум или минимум) интеграла.

Пусть критерий оптимальности 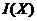представляет собой функцию одной переменной, которая достигает max при X=X⁰ (Рис. 1.5)

Очевидно, что функция 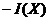достигает минимума при том же X=X⁰, а величина минимума 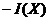равна по модулю величине максимума 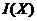и отличается только знаком, т.е. , .

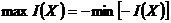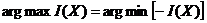Рис. 1.5

Из этих соотношений следует, что любую оптимизационную задачу можно сформулировать как определение максимумаI или минимума(-I). Причем для изменения формулировки задачи достаточно поменять знаки в критерии оптимальности. Поэтому в дальнейшем при рассмотрении общих принципов решения оптимизационных задач ограничимся лишь задачами на максимум, хотя конкретные примеры возможны и на минимум.

Оптимизационная задача должна иметь единственный критерий.

Если по смыслу задачи имеется несколько показателей, которые хотелось бы улучшить, то возможно:

1. Выбрать наиболее важный в качестве критерия и ограничить остальные некоторыми допустимыми значениями, максимальными или минимальными в зависимости от их смысла.

Например. Определить режим работы, при котором производительность установки максимальна, а себестоимость продукции не превышает допустимого значения.

2. Объединить несколько показателей в единый критерий с соответствующими весовыми коэффициентами.

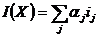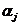, где - j-ый показатель, - коэффициент веса, причем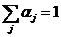

Более подробно второй подход к формулировке оптимизационных задач рассмотрен в разделе 8.

Оптимальным решением называют такой элемент множества допустимых решений D, для которого критерий принимает max значение, т.е.

, .

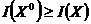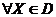Элемент называют max критерия оптимальности, а величину 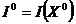- значением задачи.

Задачи оптимизации разбиваются на две группы:

1. Задачи об оптимальном решении (аргументные задачи), целью которых является нахождение значения аргумента, обеспечивающего max критерия оптимальности, т.е. нахождения .

2. Задачи об оптимальном значении (критериальные задачи), целью которых является нахождение максимума критерия оптимальности, т.е. нахождения .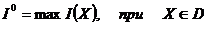

Различие между данными задачами появляется тогда, когда условия задачи заданы приближенно и существуют неточности при численном решении.

Оптимизационная задача имеет решение, если:

1.Критерий I определен на множестве D, т.е. каждому 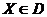соответствует единственное значение критерия.

2.Значение критерия I при 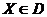ограничено сверху.

3.Множество допустимых значений D должно содержать больше одного элемента.

Простейшим решением множества D в случае целевой функции одной переменной является множество рациональных чисел, которые геометрически можно представить как точки, составляющие отрезок цифровой оси.

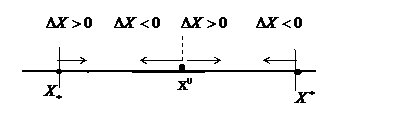
Рис. 1.6

Если точка X⁰, претендующая на максимум, находится внутри D, то для нее допустимы вариации DХ любого знака. Для граничных точек X⁰= X_* и X⁰= X^* знак вариации определен: для верхней точки DХ<0, для нижней DХ>0, т.к. при противоположных знаках значение X выйдет из области допустимых значений D (рис. 1.6).

Дата добавления: 2018-02-15; просмотров: 963; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!