Постановка задачи и ее геометрическая интерпретация
Рассмотрим задачу 
(4.1)
Где множество допустимых значений D определяется следующими условиями
(4.2) – автономные ограничения;
(4.3) – уравнения связи;
(4.4) – функциональные ограничения
Задача, определяемая выражениями (4.1) – (4.4), называется задачей математического, в общем случае нелинейного программирования. Множество D принадлежит множеству V, заданному автономными ограничениями (4.2), следовательно
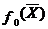
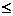
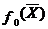(4.5).
Рассмотрим сначала упрощенную задачу, описываемую выражениями (4.1)-(4.3), т.е. в отсутствие функциональных ограничений. Графическая интерпретация для функции двух переменных, т.е. 
представлена на рис.4.1.
На плоскости варьируемых переменных X1 , X2 изображена целевая функция двух переменных 
в виде линий равного уровня. На функцию наложены автономные ограничения X i* ≤ Xi ≤ Xi*, где i=1, 2, которые определяют на плоскости область V, имеющую вид прямоугольника и ограничение типа связи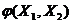 
= 0, имеющее вид кривой линии. Отрезок этой кривой, заключенный внутри прямоугольника области V и является в данном случае областью допустимых значений варьируемых переменных D, так как только точки этого отрезка удовлетворяют обоим наложенным ограничениям
Рис 4.1.
Решение данной задачи даст нам точку М1, являющуюся условным максимумом , при заданных ограничениях. Очевидно, что значение в точке М1 меньше чем в точке М, являющейся безусловным максимумом изображенной целевой функции.
|
|
|
Простейшим методом решения такой задачи является метод подстановки, при использовании которого часть варьируемых переменных выражают через другие переменные, используя уравнение связи. Так в примере 2 раздела 1.2., выразив из уравнения связи (1.5.)
где 
-длина образующей , d- диаметр днища цилиндра
получаем критерий оптимальности 
→ 
Проведя замену переменной 
можно перейти к целевой функции:
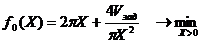
Для решения преобразованной таким образом задачи применимы любые методы определения max функции одной переменной.
При решении более сложных задач для определения условного максимума применяются методы, описанные ниже.
Суть всех методов нелинейного программирования заключается в замене исходной целевой функции, определенной на множестве D, специально сконструированной функцией, определенной на множестве V и совпадающей на множестве D с исходной целевой функцией. Таким образом, осуществляется переход от задачи определения условного max исходной целевой функции к задаче определения безусловного max специально сконструированной функции, которая может быть решена одним из методов, рассмотренных в разделе 3.
|
|
|
Разница между методами нелинейного программирования состоит в виде и способе конструирования функции, заменяющей исходную целевую функцию.
Дата добавления: 2018-02-15; просмотров: 574; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!